
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处。
海里处。
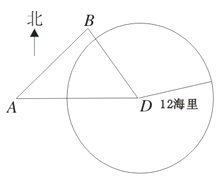
(Ⅰ)求此时该外国船只与![]() 岛的距离;
岛的距离;
(Ⅱ)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.
(参考数据: ![]() ,
, ![]() )
)
科目:高中数学 来源: 题型:
【题目】海关对同时从![]() ,
,![]() ,
,![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() ,
,![]() 均为正方形,
均为正方形,![]() ,点
,点![]() 是棱
是棱![]() 的中点.请建立适当的坐标系,求解下列问题:
的中点.请建立适当的坐标系,求解下列问题:
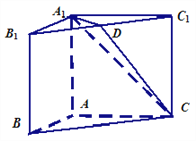
(Ⅰ)求证:异面直线![]() 与
与![]() 互相垂直;
互相垂直;
(Ⅱ)求二面角(钝角)![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() N*
N*
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知![]() (
(![]() N*),记
N*),记![]()
![]() (
(![]() 且
且![]() ),是否存在这样的常数
),是否存在这样的常数![]() ,使得数列
,使得数列![]() 是常数列,若存在,求出
是常数列,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有
 成立,求证:数列
成立,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆![]() 内”的概率.
内”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 上任意一点M满足
上任意一点M满足![]() , 其中F
, 其中F![]() (-
(-![]() F
F![]() (
(![]() 抛物线
抛物线![]() 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(I)求![]() ,
, ![]() 的标准方程;
的标准方程;
(II)请问是否存在直线l满足条件:① 过![]() 的焦点
的焦点![]() ;② 与
;② 与![]() 交于不同两点
交于不同两点![]() ,
, ![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深![]() (米)是随着一天的时间
(米)是随着一天的时间![]() 呈周期性变化,某天各时刻
呈周期性变化,某天各时刻![]() 的水深数据的近似值如下表:
的水深数据的近似值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从
①![]() , ②
, ②![]() ,③
,③![]()
![]() 中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com