
| A�� | �٢ڢ� | B�� | �ڢ� | C�� | �ڢۢ� | D�� | �ۢ� |
���� �ڢ��У���ϵͳ������ԭ��֪������һλͬѧ�ı��Ϊ20���ڢ��У�������ݵ�ƽ��������λ�����������ж϶Դ����ڢ��У����������ƽ��ֵ�������ķ��������ж϶Դ����ڢ��У��ѣ�1��3������ع�ֱ�߷��̣����ж϶Դ���
��� �⣺�ڢ��У���ϵͳ������ԭ��֪�����ļ��Ϊ52��4=13��
�ʳ�ȡ�������ı�ŷֱ�Ϊ7��7+13��7+13��2��7+13��3��
��7�š�20�š�33�š�46�ţ��ʢ��Ǽ����⣻
�ڢ��У�����1��2��3��3��4��5��ƽ����Ϊ$\frac{1}{6}$��1+2+3+4+5��=3��
��λ��Ϊ3������Ϊ3������ͬ���ʢ��������⣻
�ڢ��У������֪������ƽ��ֵΪ1������a+0+1+2+3=5�����a=-1��
�������ķ���Ϊ��$\frac{1}{5}$[��-1-1��2+��0-1��2+��1-1��2+��2-1��2+��3-1��2]=2������Ϊ$\sqrt{2}$���ʢ��Ǽ����⣻
�ڢ��У��ع�ֱ�߷���Ϊ$\widehat{y}$=bx+2��ֱ�߹��㣨$\overline{x}$��$\overline{y}$����
�ѣ�1��3������ع�ֱ�߷���$\widehat{y}$=bx+2����b=1���ʢ��������⣻
��ѡ��B��
���� ���������������жϣ��ǻ����⣬����ʱҪ�������⣬ע��ϵͳ������Ƶ�ʷֲ�ֱ��ͼ����������λ����ƽ���������Իع鷽�̵�֪ʶ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
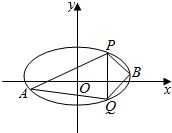 ��֪��ԲC��������ԭ�㣬������x���ϣ�������Ϊ$\frac{1}{2}$������Բ�Ķ��᳤Ϊ4$\sqrt{3}$��
��֪��ԲC��������ԭ�㣬������x���ϣ�������Ϊ$\frac{1}{2}$������Բ�Ķ��᳤Ϊ4$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\sqrt{x}$��x��1�� | B�� | $y=\sqrt{-x}$��x��-1�� | C�� | $y=\sqrt{x}$��x��0�� | D�� | $y=\sqrt{-x}$��x��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+b2����Сֵ | B�� | $\sqrt{ab}$����Сֵ | C�� | $\frac{1}{a}+\frac{1}{b}$�����ֵ | D�� | $\frac{1}{{\sqrt{a}+\sqrt{b}}}$�����ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��c��b | B�� | b��c��a | C�� | b��a��c | D�� | c��a��b |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com