
【题目】已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x .
(1)求f(log2 ![]() )的值;
)的值;
(2)求f(x)的解析式.
【答案】
(1)解:∵f(x)为奇函数,且当x∈(0,+∞)时,f(x)=2x,
∴f(log2 ![]() )=f(﹣log23)=﹣f(log23)=﹣
)=f(﹣log23)=﹣f(log23)=﹣ ![]() =﹣3
=﹣3
(2)解:设任意的x∈(﹣∞,0),则﹣x∈(0,+∞),
∵当x∈(0,+∞)时,f(x)=2x,∴f(﹣x)=2﹣x,
又f(x)是定义在R上的奇函数,则f(﹣x)=﹣f(x),
∴f(x)=﹣f(﹣x)=﹣2﹣x,即当x∈(﹣∞,0)时,f(x)=﹣2﹣x;
又f(0)=﹣f(0),f(0)=0,
综上可知,f(x)= 
【解析】(1)利用函数的奇偶性及已知表达式可得f(log2 ![]() )=f(﹣log23)=﹣f(log23)=﹣
)=f(﹣log23)=﹣f(log23)=﹣ ![]() ,再由对数运算性质可得结果;(2)设任意的x∈(﹣∞,0),则﹣x∈(0,+∞),由已知表达式可求f(﹣x),再由奇偶性可得f(x);由奇偶性易求f(0);
,再由对数运算性质可得结果;(2)设任意的x∈(﹣∞,0),则﹣x∈(0,+∞),由已知表达式可求f(﹣x),再由奇偶性可得f(x);由奇偶性易求f(0);


科目:高中数学 来源: 题型:
【题目】对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( ) 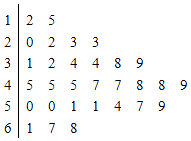
A.46 45 56
B.46 45 53
C.47 45 56
D.45 47 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是( )
①P∈a,P∈αaα
②a∩b=P,bβaβ
③a∥b,aα,P∈b,P∈αbα
④α∩β=b,P∈α,P∈βP∈b.
A.①②
B.②③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线y= ![]() x与抛物线y=
x与抛物线y= ![]() x2﹣4交于A,B两点,线段AB的垂直平分线与直线y=﹣5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为 .
x2﹣4交于A,B两点,线段AB的垂直平分线与直线y=﹣5交于Q点,当P为抛物线上位于线段AB下方(含A,B)的动点时,则△OPQ面积的最大值为 . 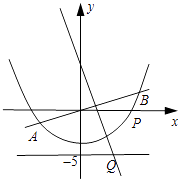
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,那么mn的最大值为( )
,2]上单调递减,那么mn的最大值为( )
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com