[题目]已知△ABC的内角A.B.C所对的边分别为a.b.c且a+2c=2bcosA．(1)求角B的大小,(2)若b=2 .a+c=4.求△ABC的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知△ABC的内角A，B，C所对的边分别为a，b，c且a+2c=2bcosA．
（1）求角B的大小；
（2）若b=2 ，a+c=4，求△ABC的面积．

【答案】
（1）解：因为a+2c=2bcosA，

由正弦定理，得sinA+2sinC=2sinBcosA，

因为C=π﹣（A+B），

所以sinA+2sin（A+B）=2sinBcosA．

即以sinA+2sinAcosB+2cosAsinB=2sinBcosA，

所以sinA（1+2cosB）=0，

因为sinA≠0，

所以cosB=﹣ ，

又因为0＜B＜π，

所以B=

（2）解：由余弦定理a2+c2﹣2accosB=b2及b=2 得，a2+c2+ac=12，

即（a+c）2﹣ac=12，

又因为a+c=4，

所以ac=4，

所以S△ABC= acsinB= ×4× =

【解析】（1）在△ABC中利用正弦定理整理已知式子可得cosB的值，根据内角的取值范围得到B。（2）利用已知根据余弦定理可推导出ac=4，进而得到三角形的面积。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，三棱锥P﹣ABC中，PA=PC，底面ABC为正三角形．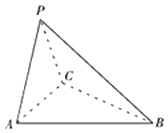

（Ⅰ）证明：AC⊥PB；
（Ⅱ）若平面PAC⊥平面ABC，AC=PC=2，求二面角A﹣PC﹣B的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，已知曲线（a为参数），直线l：x﹣y﹣6=0．
（1）在曲线C上求一点P，使点P到直线l的距离最大，并求出此最大值；
（2）过点M（﹣1，0）且与直线l平行的直线l1交C于A，B两点，求点M到A，B两点的距离之积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=xlnx﹣x﹣ （a∈R），在定义域内有两个不同的极值点x1 ， x2（x1＜x2）．
（ I）求a的取值范围；
（ II）求证：x1+x2＞2e．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=mlnx（m∈R），g（x）=cosx．
（1）若函数在（1，+∞）上单调递增，求m的取值范围；
（2）设函数φ（x）=f（x）+g（x），若对任意的，都有φ（x）≥0，求m的取值范围；
（3）设m＞0，点P（x0 ， y0）是函数f（x）与g（x）的一个交点，且函数f（x）与g（x）在点P处的切线互相垂直，求证：存在唯一的x0满足题意，且．