
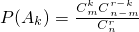 ,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=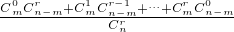 ,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断: 种情况,又从中随机取出r件产品,共有
种情况,又从中随机取出r件产品,共有 种情况,k=0,1,…,r,故其概率为
种情况,k=0,1,…,r,故其概率为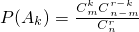 ,k=0,1,…,r.
,k=0,1,…,r.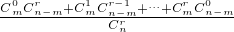 ,
,

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com