练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列满足：

    （1）求的值；

    （2）求证：数列是等比数列；

    （3）令（），如果对任意，都有，求实数的取值范围.

    【答案】（1）；（2）是以为首相为公比的等比数列；

    （3）

    【解析】

    试题分析：（1）利用赋值法，令可求；

    （2）将等式写到，再将得到的式子与已知等式联立，两式再相减，根据等比数列的定，可证明是以为首相为公比的等比数列；

    （3）由（2）可写出，利用数列的单调性当时，，当时，，因此，数列的最大值为，则可解的的范围.

    试题解析：（1）

    （2）由题可知： ①

    ②

    ②-①可得 即：，又

    ∴数列是以为首项，以为公比的等比数列

    （3）由（2）可得，

    由可得

    由可得,所以

    故有最大值

    所以，对任意，有

    如果对任意，都有，即成立，

    则，故有：，解得或

    ∴实数的取值范围是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在底面是矩形的四棱锥PABCD中，PA⊥平面ABCD，PA = AB = 2，BC = 4， E是PD的中点，

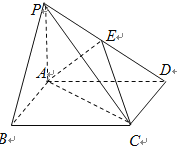
    （1）求证： 平面EAC；

    （2）求证：平面PDC⊥平面PAD；

    （3）求多面体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若a1 ， a2 ， a3 ， …a20这20个数据的平均数为 ，方差为0.21，则a1 ， a2 ， a3 ， …a20 ， 这21个数据的方差为（ ）
    A.0.19
    B.0.20
    C.0.21
    D.0.22

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个．甲、乙二人依次各抽一题．
    （1）甲抽到选择题、乙抽到判断题的概率是多少？
    （2）甲、乙二人中至少有一人抽到选择题的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆：的左顶点为，右焦点为，上顶点为，下顶点为，若直线与直线的交点为．

    （1）求椭圆的标准方程；

    （2）点为椭圆的长轴上的一个动点，过点且斜率为的直线交椭圆于两点，证明：为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知圆C的圆心在直线l：y=2x﹣4上，半径为1，点A（0，3）． （Ⅰ）若圆心C也在直线y=x﹣1上，过点A作圆C的切线，求切线的方程；
    （Ⅱ）若圆C上存在点M，使|MA|=2|MO|（O为坐标原点），求圆心C的横坐标a的取值范围．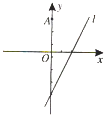

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    某园艺公司种植了一批名贵树苗，为了解树苗的生长情况，从这批树苗中随机地测量了棵树苗的高度（单位：厘米），并把这些高度列成如下的频数分布表：

    组别

    频数

    2

    4

    11

    16

    13

    4

    （Ⅰ）在这批树苗中任取一棵，其高度在厘米以上的概率大约是多少？这批树苗的平均高度大约是多少？

    （Ⅱ）为了进一步获得研究资料，标记组中的树苗为，组中的树苗为，现从组中移出一棵树苗，从组中移出两棵树苗进行试验研究，则组的树苗和组的树苗同时被移出的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在任意三角形ABC内任取一点Q，使S△ABQ≥ S△ABC的概率为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆M：（x﹣1）2+（y﹣1）2=4，直线l过点P（2，3）且与圆M交于A，B两点，且|AB|=2 ．
    （1）求直线l方程；
    （2）设Q（x0 ， y0）为圆M上的点，求x02+y02的取值范围．

    查看答案和解析>>

    同步练习册答案