
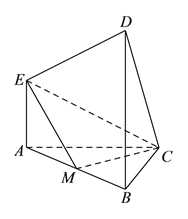
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析(2)![]() (3)点
(3)点![]() 为棱
为棱![]() 的中点.
的中点.
【解析】试题分析:(1)由等腰三角形性质得![]() ,再由
,再由![]() 平面
平面![]() ,得
,得![]() ,从而根据线面垂直判定定理得
,从而根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)利用空间向量研究二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求出两法向量夹角,最后根据二面角与法向量夹角之间关系求二面角的余弦值.(3)先设N坐标,根据向量数量积求直线
.(2)利用空间向量研究二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求出两法向量夹角,最后根据二面角与法向量夹角之间关系求二面角的余弦值.(3)先设N坐标,根据向量数量积求直线![]() 方向向量与平面
方向向量与平面![]() 法向量夹角,再根据线面角与向量夹角关系列方程,解出N坐标,最后确定N位置
法向量夹角,再根据线面角与向量夹角关系列方程,解出N坐标,最后确定N位置
试题解析:(Ⅰ)证明:∵![]() ,
, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
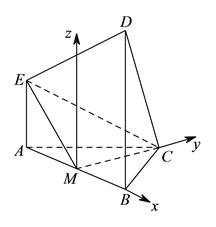
(Ⅱ)以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 为
为![]() ,
, ![]() 轴,如图建立坐标系
轴,如图建立坐标系![]() .则:
.则:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则: 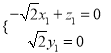 ,
,
取![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,则:
,则:

取![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
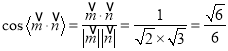 .
.
故平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.
(Ⅲ)在棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ,
,
设![]() 且
且![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
若直线![]() 与平面
与平面![]() 所成的的角为
所成的的角为![]() ,则:
,则: 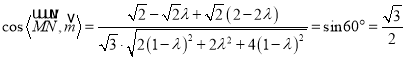 ,
,
解得![]() ,
,
所以在棱![]() 上存在一点
上存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ,
,
点![]() 为棱
为棱![]() 的中点.
的中点.


科目:高中数学 来源: 题型:
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,公比q≠1,等差数列{bn}满足b1=a1=3,b4=a2 , b13=a3 .
(1)求数列{an}与{bn}的通项公式;
(2)记cn=(﹣1)nbn+an , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:

(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在![]() 这6名学生中随机抽取3名,求至少抽到1名女生的概率.
这6名学生中随机抽取3名,求至少抽到1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com