
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 因为不共面的三个非零向量可以构成空间向量的一个基底,故只需判断三个向量是否共面即可.
解答 解:①∵{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}可以作为空间的一个基底,∴$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$不共面,∵$\overrightarrow{d}$与$\overrightarrow{c}$共线,$\overrightarrow{d}$≠0,∴$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{d}$不共面,故①正确.
②∵向量$\overrightarrow{a}$∥$\overrightarrow{b}$,∴$\overrightarrow{a}$,$\overrightarrow{b}$与任何向量都共面,∴$\overrightarrow{a}$,$\overrightarrow{b}$与任何向量都不能构成空间的一个基底,故②正确.
③∵$\overrightarrow{BA}$,$\overrightarrow{BM}$,$\overrightarrow{BN}$不能构成空间的一个基底,∴$\overrightarrow{BA}$,$\overrightarrow{BM}$,$\overrightarrow{BN}$共面,∴A,B,M,N共面,故③正确.
④∵{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,∴$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$不共面,∵$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{c}$,∴$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{m}$不共面,∴{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{m}$}也是空间的一个基底,故④正确.
故选:D.
点评 本题考查了空间向量的基本定理,共面向量的判定,是基础题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
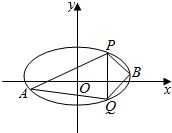 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,且椭圆的短轴长为4$\sqrt{3}$.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,且椭圆的短轴长为4$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|x|•(a-x),a∈R.
已知函数f(x)=|x|•(a-x),a∈R.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com