【题目】函数
满足以下4个条件.
①函数的定义域是
，且其图象是一条连续不断的曲线；
②函数在
不是单调函数；
③函数是偶函数；
④函数恰有2个零点.
（1）写出函数的一个解析式；
（2）画出所写函数的解析式的简图；
（3）证明满足结论③及④.
科目：高中数学 来源： 题型：
【题目】若函数
对定义域内的每一个值
，在其定义域内都存在唯一的
，使
成立，则该函数为“依附函数”.
(1)判断函数
是否为“依附函数”，并说明理由；
(2)若函数
在定义域
上“依附函数”，求
的取值范围；
(3)已知函数
在定义域
上为“依附函数”.若存在实数
，使得对任意的
，不等式
都成立，求实数
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某个比赛安排4名志愿者完成6项工作，每人至少完成一项，每项工作由一人完成，则不同的安排方式有多少种（ ）
A.7200种B.4800种C.2640种D.1560种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某观光海域AB段的长度为3百公里，一超级快艇在AB段航行，经过多次试验得到其每小时航行费用Q（单位：万元）与速度v（单位：百公里／小时）（0≤v≤3）的以下数据：
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系，现有以下三种函数模型供选择：Q＝av3＋bv2＋cv，Q＝0．5v＋a，Q＝klogav＋b．
（1）试从中确定最符合实际的函数模型，并求出相应的函数解析式；
（2）该超级快艇应以多大速度航行才能使AB段的航行费用最少？并求出最少航行费用．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国内某汽车品牌一个月内被消费者投诉的次数用
表示，据统计，随机变量的概率分布如下：
| 0 | 1 | 2 | 3 |
|
|
|
|
|
（1）求
的值；
（2）若每个月被消费者投诉的次数互不影响，求该汽车品牌在五个月内被消费者投诉3次的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】生活中万事万物都是有关联的，所有直线中有关联直线，所有点中也有相关点，现在定义：平面内如果两点
、
都在函数
的图像上，而且满足、两点关于原点对称，则称点对（、）是函数的“相关对称点对”（注明：点对（、）与（、）看成同一个“相关对称点对”）.已知函数
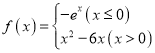，则这个函数的“相关对称点对”有（ ）
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，摩天轮的半径为
，
点距地面的高度为
，摩天轮按逆时针方向作匀速运动，且每
转一圈，摩天轮上点
的起始位置在最高点.
（1）试确定点距离地面的高度
（单位：
）关于旋转时间
（单位：
）的函数关系式；
（2）在摩天轮转动一圈内，有多长时间点距离地面超过
？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
