
����Ŀ����֪z��ʵϵ������![]() �������������ֱ������ƽ���ϵĶ�Ӧ��Ϊ
�������������ֱ������ƽ���ϵĶ�Ӧ��Ϊ![]() ��
��
��1����![]() ��ֱ��
��ֱ��![]() �ϣ���֤��
�ϣ���֤��![]() ��Բ
��Բ![]() ��
��![]() �ϣ�
�ϣ�
��2������Բ![]() ��
��![]() ��m��
��m��![]() ��
��![]() ���������Ψһ���߶�s���㣺����
���������Ψһ���߶�s���㣺����![]() ��ԲC�ϣ���
��ԲC�ϣ���![]() ���߶�s�ϣ�����
���߶�s�ϣ�����![]() ���߶�s��һ�㣨�Ƕ˵㣩����
���߶�s��һ�㣨�Ƕ˵㣩����![]() ��ԲC�ϡ�д���߶�s�ı���ʽ����˵�����ɣ�
��ԲC�ϡ�д���߶�s�ı���ʽ����˵�����ɣ�
��3���ɣ�2��֪�߶�s��ԲC֮��ȷ����һ�ֶ�Ӧ��ϵ��ͨ�����ֶ�Ӧ��ϵ���о�����д��������![]() �ǣ�1����Բ
�ǣ�1����Բ![]() �Ķ�Ӧ�߶Σ���
�Ķ�Ӧ�߶Σ���
�߶�s���߶� | m��r��ȡֵ�����ʽ |
s����ֱ��ƽ���� | |
s����ֱ��ƽ���߶� |
���𰸡�(1)������ (2) ![]() ��
��![]() ������ (3) ������
������ (3) ������
��������
��1��![]() ��ֱ��
��ֱ��![]() �ϣ�������̵����������Բ�ķ��̳�������֤��
�ϣ�������̵����������Բ�ķ��̳�������֤��![]() ��Բ
��Բ![]() ��
��![]() �ϣ�
�ϣ�
��2����������������ڶ�ԲC��![]() ��m��
��m��![]() ��
��![]() �����Ƴ�
�����Ƴ�![]() �������Ψһ���߶�s����
�������Ψһ���߶�s����![]() ���߶�s�ϣ���
���߶�s�ϣ���![]() ���߶�s��һ�㣨�Ƕ˵㣩��ʵϵ������Ϊ
���߶�s��һ�㣨�Ƕ˵㣩��ʵϵ������Ϊ![]() ��
��![]() ��ʱ
��ʱ![]() ��������̵ĸ�
��������̵ĸ�![]() �����Ƴ�
�����Ƴ�![]() ��ԲC�ϣ�
��ԲC�ϣ�
��3���ɣ�2��֪�߶�s��ԲC֮��ȷ����һ�ֶ�Ӧ��ϵ��ֱ����д����
��1��������ɵ�![]() ��
��
�ⷽ��![]() ����
����![]()
���![]() ��
��![]() ��
��
��Ϊ![]() ��
��
��![]() ��Բ
��Բ![]() ��
��![]() ��
��
��2����![]() ����
����![]() ʱ��
ʱ��
���![]() ��
��
���![]() ��
��![]() ��
��
������ɵ�![]() ��
��
�������![]() ��
��
��![]() ��
��![]() ����
����![]()
���߶�sΪ��![]() ��
��![]()
��![]() ���߶�s��һ�㣨�Ƕ˵㣩��
���߶�s��һ�㣨�Ƕ˵㣩��
��ʵϵ������Ϊ![]() ��
��![]()
��ʱ![]() ���ҵ�
���ҵ�![]()
![]() ��ԲC��
��ԲC��
��3����
�߶�s���߶� | m��r��ȡֵ�����ʽ |
s����ֱ��ƽ���� |
|
s����ֱ��ƽ���߶� |
|
�߶�s���߶� |
|


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ������
������![]() ����
����![]() .
.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2������![]() ����
����![]() ������ǰn���Ϊ
������ǰn���Ϊ![]() ��������������n��ʹ����ʽ
��������������n��ʹ����ʽ![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������Ͷ��2�Σ��۲���ֵĵ��������ǵ�һ�γ��ֵĵ���Ϊ![]() ���ڶ��γ��ֵĵ���Ϊ
���ڶ��γ��ֵĵ���Ϊ![]() ���Ծͷ�����
���Ծͷ�����![]() ������и��⣺
������и��⣺
��1������ֻ��һ����ĸ��ʣ�
��2������ֻ��������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
������![]() ��
��![]() �ڵ����ݼ�����ʵ��
�ڵ����ݼ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������![]() ��������ֵ��ֱ�Ϊ
��������ֵ��ֱ�Ϊ![]() ��
��![]() ��֤����
��֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У���OΪ���㣬x��������Ϊ���Ὠ��������ϵ����֪����C�ļ����귽��Ϊ����1-cos2����=8cos����ֱ����cos��=1������C�ཻ��M��N���㣬ֱ��l������P��2��0������б��Ϊ����l������C��A��B���㣮
��1��������C����ֱ�����귽�̣�����|MN|��ֵ��
��2����|PA|��|MN|��|PB|�ɵȱ����У���ֱ��l����б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��������ֱ��![]() ��
��![]() �ཻ�ڵ�O������ƽ��������һ��M����x��y�ֱ���M��ֱ��
�ཻ�ڵ�O������ƽ��������һ��M����x��y�ֱ���M��ֱ��![]() ��
��![]() �ľ��룬�������Ǹ�ʵ���ԣ�x��y���ǵ�M�ġ��������ꡱ����֪����p��0��q��0�����������������⣺
�ľ��룬�������Ǹ�ʵ���ԣ�x��y���ǵ�M�ġ��������ꡱ����֪����p��0��q��0�����������������⣺

����p=q=0���������ꡱΪ��0��0���ĵ�����ֻ��1����
����pq=0����p+q��0���������ꡱΪ��p��q���ĵ�����ֻ��2����
����pq��0�������ꡱΪ��p��q���ĵ�����ֻ��4����
���������У���ȷ�������______����д��������ȷ�������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���賣��![]() ����֪����
����֪����![]() ��
��![]() ��
��![]() ������
������![]() ��Ϊʵ����
��Ϊʵ����![]() Ϊ������λ���Ҷ������⸴��
Ϊ������λ���Ҷ������⸴��![]() ����
����![]() ����
����![]() ����
��Ϊ��![]() �����꣬
�����꣬![]() ��Ϊ��
��Ϊ��![]() �����꣬ͨ����ϵʽ
�����꣬ͨ����ϵʽ![]() �����Կ���������ƽ���ϵ��һ���任������ƽ���ϵĵ�
�����Կ���������ƽ���ϵ��һ���任������ƽ���ϵĵ�![]() �䵽���ƽ���ϵĵ�
�䵽���ƽ���ϵĵ�![]() .
.
��1���ֱ�д��![]() ��
��![]() ��
��![]() ��ʾ�Ĺ�ϵʽ��
��ʾ�Ĺ�ϵʽ��
��2����![]() ������
������![]() ��Բ
��Բ![]() ���ƶ�ʱ����֤����
���ƶ�ʱ����֤����![]() ���ñ任��õ��ĵ�
���ñ任��õ��ĵ�![]() ����һ��Բ�ϣ��������Բ�ķ��̣�
����һ��Բ�ϣ��������Բ�ķ��̣�
��3����֤����������ij���![]() ���ܴ�������
���ܴ�������![]() ��ʹ�õ���
��ʹ�õ���![]() ��
��![]() ���ƶ�ʱ����
���ƶ�ʱ����![]() ������任��õ��ĵ�
������任��õ��ĵ�![]() �Ĺ켣�Ƕ��κ���
�Ĺ켣�Ƕ��κ���![]() ��ͼ��д������������
��ͼ��д������������![]() ����������������
����������������![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����FΪ��ԲC��![]() (a��b��0)���㣬��A��B�ֱ�Ϊ��ԲC���Ҷ�����϶��㣬��P(
(a��b��0)���㣬��A��B�ֱ�Ϊ��ԲC���Ҷ�����϶��㣬��P(![]() ��
��![]() )����ԲC�ϣ�������OP��AB��
)����ԲC�ϣ�������OP��AB��
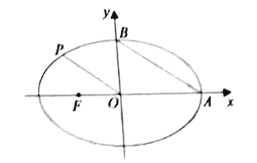
��1������ԲC�ķ��̣�
��2��������F��ֱ��l����ԲC��D��E���㣨��Dλ��x���Ϸ�����ֱ��AD��AE��б�ʷֱ�Ϊ![]() ��
��![]() ��������
��������![]() ��
��![]() ����2����ֱ��l�ķ��̣�
����2����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������ԭ��
Ϊ����������ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ��������Ϊ���Ὠ��������ϵ������
��������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��![]() .
.
��1����![]() ʱ���ж�����
ʱ���ж�����![]() ������
������![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
��2��������![]() ������ֻ��һ�㵽����
������ֻ��һ�㵽����![]() �ľ������
�ľ������![]() ʱ��������
ʱ��������![]() �ϵ�����
�ϵ�����![]() ����Ϊ
����Ϊ![]() �ĵ������.
�ĵ������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com