
【题目】在极坐标系中,圆C的圆心坐标为(1,0),半径为1.
(1)求圆C的极坐标方程;
(2)若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.已知直线l的参数方程为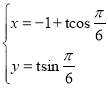 (t为参数),试判断直线l与圆C的位置关系.
(t为参数),试判断直线l与圆C的位置关系.
【答案】(1)ρ=2cosθ(2)相切
【解析】
(1)作图设点,根据极坐标中点的坐标的意义,求圆在极坐标下的轨迹方程;
(2)将直线和曲线都化为普通方程,在直角坐标系下进行判断.
(1)如图,设M(ρ,θ)为圆C上除点O,B外的任意一点,连结OM,BM,在Rt△OBM中,
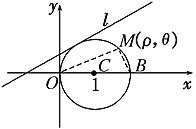
|OM|=|OB|cos∠BOM,
所以ρ=2cosθ.
可以验证点O(0,![]() ),B(2,0)也满足ρ=2cosθ,
),B(2,0)也满足ρ=2cosθ,
故ρ=2cosθ为所求圆的极坐标方程.
(2)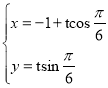
得直线l的普通方程为y=![]() (x+1),
(x+1),
即直线l的普通方程为x-![]() y+1=0.
y+1=0.
由ρ=2cosθ,得圆C的直角坐标方程为(x-1)2+y2=1.
因为圆心C到直线l的距离d=![]() =1,
=1,
所以直线l与圆C相切.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
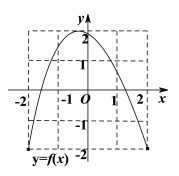
【题目】如图分别为定义域和值域均为![]() 的函数
的函数![]() 和函数
和函数![]() 的图象,则下列命题正确的是( )
的图象,则下列命题正确的是( )
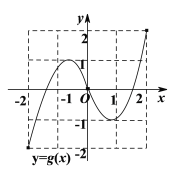
A.函数![]() 恰有
恰有![]() 个零点B.函数
个零点B.函数![]() 恰有
恰有![]() 个零点
个零点
C.函数![]() 恰有
恰有![]() 个零点D.函数
个零点D.函数![]() 恰有
恰有![]() 个零点
个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题“若△ABC的三个内角构成等差数列,则△ABC必有一内角为![]() ”的否命题( )
”的否命题( )
A.与原命题真假相异B.与原命题真假相同
C.与原命题的逆否命题的真假不同D.与原命题的逆命题真假相异
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
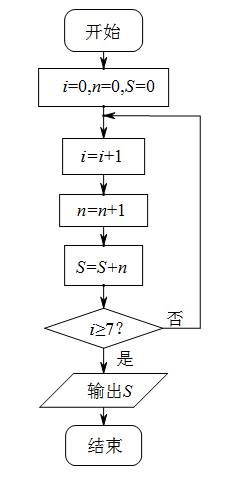
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人玩摸球游戏,每两局为一轮,每局游戏的规则如下:甲,乙两人均从装有4只红球、1只黑球的袋中轮流不放回摸取1只球,摸到黑球的人获胜,并结束该局.
(1)若在一局中甲先摸,求甲在该局获胜的概率;
(2)若在一轮游戏中约定:第一局甲先摸,第二局乙先摸,每一局先摸并获胜的人得1分,后摸井获胜的人得2分,未获胜的人得0分,求此轮游戏中甲得分X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com