
【题目】设等差数列{an}满足 ![]() =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
【答案】C
【解析】解:∵等差数列{an}满足 ![]() =1, ∴(sina3cosa6﹣sina6cosa3)(sina3cosa6+sina6cosa3)
=1, ∴(sina3cosa6﹣sina6cosa3)(sina3cosa6+sina6cosa3)
=sin(a3+a6)=(sina3cosa6+sina6cosa3),
∴sina3cosa6﹣sina6cosa3=1,
即sin(a3﹣a6)=1,或sin(a3+a6)=0(舍)
当sin(a3﹣a6)=1时,
∵a3﹣a6=﹣3d∈(0,3),a3﹣a6=2kπ+ ![]() ,k∈Z,
,k∈Z,
∴﹣3d= ![]() ,d=﹣
,d=﹣ ![]() .
.
∵ ![]() =
= ![]() +(a1﹣
+(a1﹣ ![]() )n,
)n,
且仅当n=9时,数列{an}的前n项和Sn取得最大值,
∴﹣ ![]() =9,化为
=9,化为 ![]() .
.
∴ ![]() =
= ![]() .
.
故选:C.
由已知条件推导出sin(a3﹣a6)=1,或sin(a3+a6)=0,由仅当n=9时,数列{an}的前n项和Sn取得最大值,推导出 ![]() .由此能求出该数列首项a1的取值范围.
.由此能求出该数列首项a1的取值范围.


科目:高中数学 来源: 题型:
【题目】等差数列{an}中,已知an>0,a1+a2+a3=15,且a1+2,a2+5,a3+13构成等比数列{bn}的前三项.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1、A2为椭圆 ![]() 的左右顶点,若在椭圆上存在异于A1、A2的点P,使得
的左右顶点,若在椭圆上存在异于A1、A2的点P,使得 ![]() ,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC= ![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.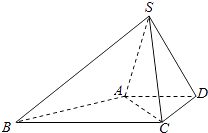
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,且(n+1)an=2Sn(n∈N*),数列{bn}满足 ![]() ,
, ![]() ,对任意n∈N* , 都有
,对任意n∈N* , 都有 ![]() .
.
(1)求数列{an}、{bn}的通项公式;
(2)令Tn=a1b1+a2b2+…+anbn . 若对任意的n∈N* , 不等式λnTn+2bnSn<2(λn+3bn)恒成立,试求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率. 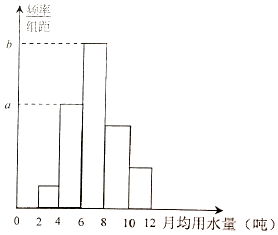
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数α,使得sinα+cosα= ![]() ;
;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴方程;
的一条对称轴方程;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称图形.
成中心对称图形.
其中命题正确的是(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com