练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．若函数f（x）=3x2-5x+a的两个零点分别为x1，x2．且有-2＜x1＜0与1＜x2＜3，试求出a的取值范围．

    分析 由条件利用二次函数的性质求得实数a的取值范围．

    解答 解：∵f（x）=3x2-5x+a，
    ∴f（x）的图象是开口向上的抛物线．
    由题意得：$\left\{\begin{array}{l}{f（-2）＞0}\\{f（0）＜0}\\{f（1）＜0}\\{f（3）＞0}\end{array}\right.$，即$\left\{\begin{array}{l}{12+10+a＞0}\\{a＜0}\\{3-5+a＜0}\\{23-15+a＞0}\end{array}\right.$解的-8＜a＜0，
    故a的取值范围为（-8，0）．

    点评 本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．（1）求函数f（x）=ln（$\sqrt{3}$-2cosx）的定义域；
    （2）求函数f（x）=2cos2x+3sinx-5的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

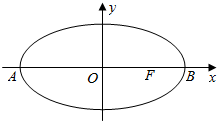    14．在平面直角坐标系xOy中，如图，已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B，右焦点为F．设过点T（t，m）的直线TA、TB与椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0．
    （1）设动点P满足PF2-PB2=4，求点P的轨迹；
    （2）设${x_1}=2，{x_2}=\frac{1}{3}$，求点T的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列各数中最小的数是（　　）
    A．111 111（2）B．210（6）C．1 000（4）D．110（8）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知定义在R上的偶函数，f（x）在x≥0时，f（x）=ex+ln（x+1），若f（a）＜f（a-1），则a的取值范围是（　　）
    A．（-∞，1）B．（-∞，$\frac{1}{2}$）C．（$\frac{1}{2}$，1）D．（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知A={x|a≤x≤a+3}，B={x|x＜-1或x＞5}，若A∪B=B，则实数a的取值范围是（-∞，-4）∪（5，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．长、宽、高分别为3，4，5的长方体，沿相邻面对角线截取一个三棱锥（如图），剩下几何体的体积为50．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设函数$f（x）=\left\{\begin{array}{l}\sqrt{x-1}（x＞1）\\ sin\frac{πx}{2}（x≤1）\end{array}\right.$，则f[f（2）]=（　　）
    A．0B．1C．2D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知x+x-1=3，则代数式$\frac{{x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}}}{{x}^{2}+{x}^{-2}}$的值是$\frac{\sqrt{5}}{7}$．

    查看答案和解析>>

    同步练习册答案