
【题目】已知下列命题:
①在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() ,若
,若![]() 在
在![]() 内取值范围概率为
内取值范围概率为![]() ,则
,则![]() 在
在![]() 内取值的概率为
内取值的概率为![]() ;
;
②若![]() ,
,![]() 为实数,则“
为实数,则“![]() ”是“
”是“![]() ”的充分而不必要条件;
”的充分而不必要条件;
③已知命题![]() ,
,![]() ,则
,则![]() 是:
是:
![]() ,
,![]() ;
;
④![]() 中,“角
中,“角![]() ,
,![]() ,
,![]() 成等差数列”是“
成等差数列”是“![]() ”的充分不必要条件;其中,所有真命题的个数是( )
”的充分不必要条件;其中,所有真命题的个数是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
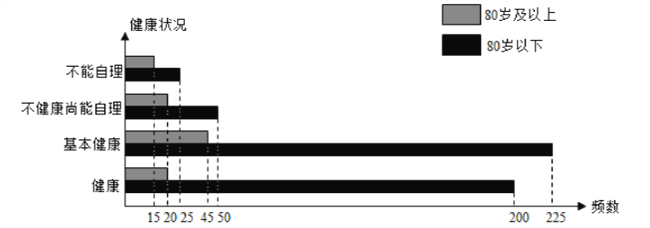
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.
利用样本估计总体,试估计政府执行此计划的年度预算.(单位:亿元,结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010-2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,连接器行业增长呈现加速状态.根据该折线图,下列结论正确的个数为( )

①每年市场规模量逐年增加;
②增长最快的一年为2013~2014;
③这8年的增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() 年
年![]() 月份,某市街头出现共享单车,到
月份,某市街头出现共享单车,到![]() 月份,根据统计,市区所有人骑行过共享单车的人数已占
月份,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是大学生(含大中专及高职),该市区人口按
是大学生(含大中专及高职),该市区人口按![]() 万计算,大学生人数约
万计算,大学生人数约![]() 万人.
万人.
(1)任选出一名大学生,求他(她)骑行过共享单车的概率;
(2)随单车投放数量增加,乱停乱放成为城市管理的问题,以下是累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间的关系图表:
之间的关系图表:
累计投放单车数量 |
|
|
|
|
|
乱停乱放单车数量 |
|
|
|
|
|
①计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
②已知该市共有五个区,其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中,检查组随机抽取三个区调查单车乱停乱放数量, ![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘法估计公式分别为
中的斜率和截距的最小二乘法估计公式分别为
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com