
对于平面直角坐标系内的任意两点 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: .给出下列三个命题:
.给出下列三个命题:
①若点C在线段AB上,则 ;
;
②在 中,若∠C=90°,则
中,若∠C=90°,则 ;
;
③在 中,
中, .
.
其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:①若点C在线段AB上,设点C(x0,y0)那么x0在x1,x2之间.y0在y1,y2之间,所以||AC||+||CB||=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=||AB||正确;
②平方后不能消除x0,y0,命题不成立;
③不妨假设C角为直角,以A为原点,AC所在直线为x轴,作直角坐标,得A(0 , 0 )、B( ),点C(
),点C( ,0)。代入③式中得:︱
,0)。代入③式中得:︱ ︱+︱
︱+︱ ︱=︱
︱=︱ ︱+︱
︱+︱ ︱,所以③不成立。故选B.
︱,所以③不成立。故选B.
考点:本题考查两点间的距离公式。
点评:本题是新运算与绝对值的结合,应注意点C的不同位置。弄清新命题的运算规则,是本题的关键点;设出各点坐标,代入关系式计算,根据计算结果进行判断是做本题的基本前提。


科目:高中数学 来源: 题型:单选题
若点 和点
和点 分别为双曲线
分别为双曲线 (
( )的中心和左焦点,点
)的中心和左焦点,点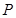 为双曲线右支上的任意一点,则
为双曲线右支上的任意一点,则 的取值范围为( )
的取值范围为( )
A.[3-  , ,  ) ) | B.[3+  , ,  ) ) |
C.[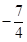 , ,  ) ) | D.[ , ,  ) ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com