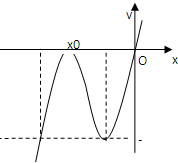
解:(1)依题意,函数f(x)的图象如图所示,
f'(x)=3x
2+2bx+c∵原点不是切点,∴c≠0.
记切点横坐标为x
0(x
0<0)
又f(x)=x
3+bx
2+cx=x(x
2+bx+c)
则方程x
2+bx+c=0有且仅有一个根x=x
0∴△=b
2-4c=0,即
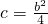
.①
∴
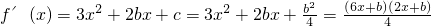
则
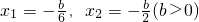
∴
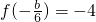
,即5b
2-36bc+432=0.②
由①②,解得b=6,c=9
(2)f(x)=x
3+6x
2+9x,由f(x)=-4得x=-4或-1.∴当a<-4时,f(x)在[a,0]上的最小值F(a)=f(a)=a
3+6a
2+9a
当-4≤a≤1时,f(x)在[a,0]上的最小值F(a)=f(-1)=-4
当1<a<0时,f(x)在[a,0]上的最小值F(a)=f(a)=a
3+6a
2+9a
要使F(a)≤λa恒成立,只需
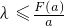
恒成立,∴当a<-4时,
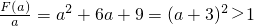
,则λ≤1
当1<a<0时,
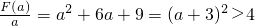
则λ≤4
当-4≤a≤-1时,
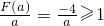
,则λ≤1
综上所述,λ≤1
(3)由(2)知,当-1<x<0,f(x)<4x恒成立
(或利用f(x)-4x=x
3+6x
2+5x=x(x+1)(x+5)<0在-1<x<0,恒成立)
记g(x)=x-sinx(-1<x<0),
则g'(x)=1-cosx>0.∴g(x)在(-1,0)上单调递增,g(x)<g(0)=0.
∴x<sinx在-1<x<0恒成立,∴-1<x<0时,在f(x)≤4x<4sinx,得证
分析:(1)根据f(x)=x
3+bx
2+cx的图象与x轴相切于非原点的一点,可以判断c≠0.且当x小于0时有一个极值为0,结合图象可得方程x
2+bx+c=0有且仅有一个根,且在这个根处导数等于0,据此可求出b,c的值.
(2)先求函数的导数,令导数等于0,求出极值点,再按a的取值讨论求出函数在[a,0]上的最小值,代入F(a)≤λa,求λ的取值范围.
(3)由(2)知,当-1<x<0,f(x)<4x恒成立,所以可用放缩法,证明4x<4sinx即可,再转换为判断函数y=4x-4sinx与0的大小比较,借助导数求出.
点评:本题主要考查了导数与函数的极值,最值,以及单调性的判断之间的关系,属于导数的应用题.

 解:(1)依题意,函数f(x)的图象如图所示,
解:(1)依题意,函数f(x)的图象如图所示,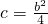 .①
.①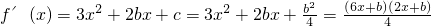
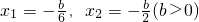 ∴
∴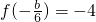 ,即5b2-36bc+432=0.②
,即5b2-36bc+432=0.②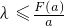 恒成立,∴当a<-4时,
恒成立,∴当a<-4时,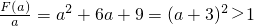 ,则λ≤1
,则λ≤1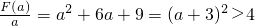 则λ≤4
则λ≤4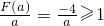 ,则λ≤1
,则λ≤1

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<