
【题目】对正整数n,有抛物线y2=2(2n﹣1)x,过P(2n,0)任作直线l交抛物线于An , Bn两点,设数列{an}中,a1=﹣4,且an= ![]() (其中n>1,n∈N),则数列{an}的前n项和Tn=( )
(其中n>1,n∈N),则数列{an}的前n项和Tn=( )
A.4n
B.﹣4n
C.2n(n+1)
D.﹣2n(n+1)
科目:高中数学 来源: 题型:
【题目】下列命题中是真命题的个数是( )
(1)垂直于同一条直线的两条直线互相平行
(2)与同一个平面夹角相等的两条直线互相平行
(3)平行于同一个平面的两条直线互相平行
(4)两条直线能确定一个平面
(5)垂直于同一个平面的两个平面平行
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若方程f(x)=x有三个不同的解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB,CD的长度分别为2 ![]() 和4
和4 ![]() ,M,N分别是AB,CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
,M,N分别是AB,CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB,CD可能相交于点M;
②弦AB,CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
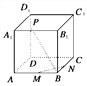
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}(n≥1,n∈N)满足a1=2,a2=6,且(an+2﹣an+1)﹣(an+1﹣an)=2,若[x]表示不超过x的最大整数,则[ ![]() +
+ ![]() +…+
+…+ ![]() ]= .
]= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com