选修4 - 4：坐标系与参数方程
在直角坐标系xOy中，直线l的方程是y = 8，圆C的参数方程是
（φ为参数）。以O为极点，x轴的非负半轴为极轴建立极坐标系。
（Ⅰ）求直线l和圆C的极坐标方程；
（Ⅱ）射线OM：θ = α（其中
）与圆C交于O、P两点，与直线l交于点M，射线ON：
与圆C交于O、Q两点，与直线l交于点N，求
的最大值.
第1卷单元月考期中期末系列答案科目：高中数学 来源：2017届广东中山一中高三上学期统测二数学（文）试卷（解析版） 题型：解答题
选修4—4：坐标系与参数方程
已知平面直角坐标系
，以
为极点，
轴的非负半轴为极轴建立极坐标系，
点的极坐标为
，曲线
的参数方程为
（
为参数）.
（1）写出点
的直角坐标及曲线
的直角坐标方程；
（2）若
为曲线
上的动点，求
中点
到直线
的距离的最小值.
查看答案和解析>>
科目：高中数学 来源：2017届河南开封市高三上10月月考数学（文）试卷（解析版） 题型：选择题
双曲线C：
的左、右焦点分别为
，
，M，N两点在双曲线C上，且MN∥F1F2，
，线段F1N交双曲线C于点Q，且
，则双曲线C的离心率为
A.2 B.
C.
D.
查看答案和解析>>
科目：高中数学 来源：2017届河南开封市高三上10月月考数学（理）试卷（解析版） 题型：解答题
随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：
性别与读营养说明列联表：
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
（Ⅰ）根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？
（Ⅱ）从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数
的分布列及其均值（即数学期望）．
（注：
，其中
为样本容量．）
查看答案和解析>>
科目：高中数学 来源：2017届河南开封市高三上10月月考数学（理）试卷（解析版） 题型：选择题
双曲线C：
的左、右焦点分别为
，
，M，N两点在双曲线C上，且MN∥F1F2，
，线段F1N交双曲线C于点Q，且
，则双曲线C的离心率为
A.2 B.
C.
D.
查看答案和解析>>
科目：高中数学 来源：2016届广东汕头市普通高考高三第二次模拟数学（文）试卷（解析版） 题型：解答题
已知四棱锥
中,
垂直于直角梯形
所在的平面,
是
的中点, 且
.
（1）求证：
平面
；
（2）求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源：2016-2017学年甘肃省高一上学期第一次阶段考数学试卷（解析版） 题型：解答题
某化工厂生产的一种溶液，按市场要求，杂质含量不能超过0．1%，若刚开始杂质含量是2%，每过滤一次可使杂质含量减少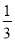
，问至少要过滤几次才能使产品达到市场要求（
）
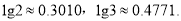查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，若
，则
（ ）
B.
