
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的实轴长为4,焦距为
的实轴长为4,焦距为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线l经过点![]() 且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为
且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为![]() ,
,![]() ,试问:是否存在点Q,使得
,试问:是否存在点Q,使得![]() 为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测
,并预测![]() 地区2019年足球特色学校的个数(精确到个).
地区2019年足球特色学校的个数(精确到个).
本题参考公式和数据: ,
,![]() ,
,![]() ,
,![]() ,
,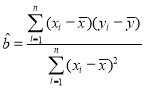 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:![]() ,并绘制出频率分布直方图,如图所示.
,并绘制出频率分布直方图,如图所示.

(1)求频率分布直方图中![]() 的值,并估计该市高中学生的平均成绩;
的值,并估计该市高中学生的平均成绩;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 四名学生的考试成绩在区间
四名学生的考试成绩在区间![]() 内,
内,![]() 、
、![]() 两名学生的考试成绩在区间
两名学生的考试成绩在区间![]() 内,现从这6名学生中任选两人参加座谈会,求学生
内,现从这6名学生中任选两人参加座谈会,求学生![]() 、
、![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角三角形ABC中,![]() ,
,![]() (如右图所示)
(如右图所示)
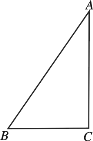
(Ⅰ)若以AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(Ⅱ)一只蚂蚁在问题(Ⅰ)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com