
(本小题满分12分) 已知点 ,直线
,直线 及圆
及圆 .
.
(1)求过 点的圆的切线方程;
点的圆的切线方程;
(2)若直线 与圆相切,求
与圆相切,求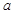 的值;
的值;
(3)若直线 与圆相交于
与圆相交于 两点,且弦
两点,且弦 的长为
的长为 ,求
,求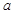 的值.
的值.
(1) x=3或3x-4y-5=0.(2) a=0或a=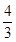 . (3) a=-
. (3) a=-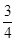 .
.
解析试题分析:(1)研究过一点的圆的切线方程问题,要确定点的位置,是否为圆上的点,然后确定直线的斜率是否存在两种情况分析得到结论。
(2)因为直线与圆相切,那么则有圆心到直线的距离等于圆的半径,得到结论。
(3)结合圆的半径和半弦长和弦心距的勾股定理求解得到参数的值。
解:(1)由题意可知M在圆(x-1)2+(y-2)2=4外,
故当x=3时满足与圆相切. ﹍﹍﹍﹍﹍﹍﹍1分
当斜率存在时设为y-1=k(x-3),即kx-y-3k+1=0.
由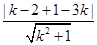 =2,∴k=
=2,∴k=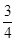 , ﹍﹍﹍﹍﹍﹍﹍4分
, ﹍﹍﹍﹍﹍﹍﹍4分
∴所求的切线方程为x=3或3x-4y-5=0. ﹍﹍﹍﹍﹍﹍﹍5分
(2)由ax-y+4=0与圆相切知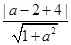 =2, ﹍﹍﹍﹍﹍﹍﹍7分
=2, ﹍﹍﹍﹍﹍﹍﹍7分
∴a=0或a=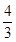 . ﹍﹍﹍﹍﹍﹍﹍9分
. ﹍﹍﹍﹍﹍﹍﹍9分
(3)圆心到直线的距离d=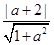 , ﹍﹍﹍﹍﹍﹍﹍10分
, ﹍﹍﹍﹍﹍﹍﹍10分
又l=2 ,r=2,
,r=2,
∴由r2=d2+( )2,可得a=-
)2,可得a=-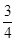 . ﹍﹍﹍﹍﹍﹍﹍12分
. ﹍﹍﹍﹍﹍﹍﹍12分
考点:本试题主要是考查了直线与圆的位置关系的综合运用。重点是求解相切的情况,以及相交时的弦长问题的运用。
点评:解决该试题的关键是能利用直线与圆的位置关系的判定,那就是圆心到直线的距离和原点半径的关系来得到关系式,进而求解。


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
(本题满分15分)
设有半径为3 的圆形村落,
的圆形村落,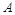 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 一直向北直行;
一直向北直行;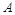 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝 所在的方向前进。
所在的方向前进。
(1)若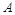 在距离中心5
在距离中心5 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,
求: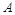 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程
(2)设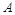 、
、 两人速度一定,其速度比为
两人速度一定,其速度比为 ,且后来
,且后来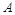 恰与
恰与 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?
(以村落中心为参照,说明方位和距离)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与
轴上,圆心的横坐标是整数,且与 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线
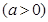 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com