
【题目】运行如图的程序,如果输入的m,n的值分别是24和15,记录输出的i和m的值.在平面直角坐标系xOy中,已知点A(i﹣4,m),圆C的圆心在直线l:y=2x﹣4上. 
(1)若圆C的半径为1,且圆心C在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使∠OMA=90°,求圆C的半径r的最小值.
【答案】
(1)解:根据题意可得,i=4,m=3,∴A(0,3).
由 ![]() 得圆心C为(3,2),
得圆心C为(3,2),
∵圆C的半径为1,∴圆C的方程为:(x﹣3)2+(y﹣2)2=1.
显然切线的斜率一定存在,设所求圆C的切线方程为y=kx+3,即kx﹣y+3=0,
则 ![]() ,即
,即 ![]() ,∴2k(4k+3)=0
,∴2k(4k+3)=0
∴k=0或者 ![]() ,
,
∴所求圆C的切线方程为:y=3或者 ![]() ,
,
即y=3或者3x+4y﹣12=0.
(2)解:依题意,点M在以OA为直径的圆上,其圆心为D ![]() ,半径为
,半径为 ![]() ,
,
点M也在圆C上,∴点M是圆D和圆C的公共点,
又圆C的圆心在直线l:y=2x﹣4上,∴要使圆C的半径最小,只须过点D作直线l的垂线,以垂足为圆心C并与圆D外切时的圆C的半径r最小,
∵点D到直线l的距离d= ![]() ,
,
∴圆C的半径r最小值为 ![]() .
.
【解析】根据题意可得,i=4,m=3,即A(0,3),(1)联立 ![]() 得圆心C为(3,2),则圆C的方程为:(x﹣3)2+(y﹣2)2=1,显然切线的斜率一定存在,设所求圆C的切线方程为y=kx+3,即kx﹣y+3=0,由点到直线的距离公式,可得到k的值,则所求圆C的切线方程可求;(2)依题意,点M在以OA为直径的圆上,其圆心为D
得圆心C为(3,2),则圆C的方程为:(x﹣3)2+(y﹣2)2=1,显然切线的斜率一定存在,设所求圆C的切线方程为y=kx+3,即kx﹣y+3=0,由点到直线的距离公式,可得到k的值,则所求圆C的切线方程可求;(2)依题意,点M在以OA为直径的圆上,其圆心为D ![]() ,半径为
,半径为 ![]() ,点M也在圆C上,得到点M是圆D和圆C的公共点,又圆C的圆心在直线l:y=2x﹣4上,要使圆C的半径最小,只须过点D作直线l的垂线,以垂足为圆心C并与圆D外切时的圆C的半径r最小,由点D到直线l的距离即可得圆C的半径r最小值.
,点M也在圆C上,得到点M是圆D和圆C的公共点,又圆C的圆心在直线l:y=2x﹣4上,要使圆C的半径最小,只须过点D作直线l的垂线,以垂足为圆心C并与圆D外切时的圆C的半径r最小,由点D到直线l的距离即可得圆C的半径r最小值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 和直线
和直线![]() .
.
(Ⅰ)求![]() 的参数方程以及圆
的参数方程以及圆![]() 上距离直线
上距离直线![]() 最远的点
最远的点![]() 坐标;
坐标;
(Ⅱ)以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,将圆
轴正半轴为极轴建立极坐标系,将圆![]() 上除点
上除点![]() 以外所有点绕着
以外所有点绕着![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() ,求曲线
,求曲线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,
中, ![]() ,且
,且![]() 的等比中项为
的等比中项为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出正整数
恒成立?若存在,求出正整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 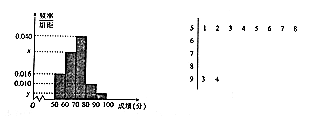
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com