
����Ŀ��ij�̳����д�����������������䣬![]() ������һ����
������һ����![]() ������������
������������![]() ������������
������������![]() �������ĸ�����
�������ĸ�����![]() �����������
�����������![]() �����������
�����������![]() ������ÿ��������Żأ����Ѷ���
������ÿ��������Żأ����Ѷ���![]() Ԫ��һ��
Ԫ��һ��![]() �����������ᣬ���Ѷ���
�����������ᣬ���Ѷ���![]() Ԫ��һ��
Ԫ��һ��![]() �����������ᣬ���������ֵ������н�����
�����������ᣬ���������ֵ������н�����![]() ������
������![]() Ԫ����
Ԫ����![]() ������
������![]() Ԫ����
Ԫ����![]() ������
������![]() Ԫ������������û�н���.
Ԫ������������û�н���.
����ͳ�ƣ����Ѷ�![]() ������̬�ֲ�
������̬�ֲ�![]() ��ij����
��ij����![]() Ϊ�˿ͣ���������Ѷ�
Ϊ�˿ͣ���������Ѷ�![]() ����λ��Ԫ��������
����λ��Ԫ��������![]() �ڲ��н���������
�ڲ��н���������
����ij��λ�˿���һ��![]() �����������ᣬ�������н�����
�����������ᣬ�������н�����![]() �ķֲ��У�
�ķֲ��У�
����ij�˿����Ѷ�Ϊ![]() Ԫ����������������������һ������
Ԫ����������������������һ������![]() �������������������һ��
�������������������һ��![]() �����������ᣬ���ʣ���λ�˿�ѡ��һ�ַ������ý��������ֵ�ϴ�.
�����������ᣬ���ʣ���λ�˿�ѡ��һ�ַ������ý��������ֵ�ϴ�.
������![]() ����
����![]()
���𰸡�(��)286;(��)�𰸼�������(��)��λ�˿�ѡ���������õ�����ֵ�ϴ�.
��������
�������������������æ�=150����2=625���æ�=25��100=�̩�2�ң����Ѷ�X�����䣨100��150]�ڵĹ˿���һ��A�����������ᣬ�н���Ϊ0.6������ԼΪ1000��P���̩�2�ң�X���̣����ɵ������н���������
������λ�˿�ÿ��һ��A���������н��ʶ�Ϊ0.6���������н������η��Ӷ���ֲ�B��3��0.6����![]() ����k=0��1��2��3�������ɵó���
����k=0��1��2��3�������ɵó���
������������ѧ�����ļ��㹫ʽ���ɵó���
���������
�����������![]() ����
����![]() ��
��
���Ѷ�![]() ������
������![]() �ڵĹ˿���һ��
�ڵĹ˿���һ��![]() �����������ᣬ�н���Ϊ
�����������ᣬ�н���Ϊ![]() ��
��
����ԼΪ![]() �ˣ�
�ˣ�
�����н�������ԼΪ![]() �ˣ�
�ˣ�
������λ�˿�ÿ��һ��![]() ���������н��ʶ�Ϊ
���������н��ʶ�Ϊ![]() ��
��
�������н�����![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]()
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
 ����
����![]() ����һ�����ý��������ֵΪ
����һ�����ý��������ֵΪ![]() ��
��
![]() ����һ�����ý��������ֵΪ
����һ�����ý��������ֵΪ![]() ��
��
����һ���ý��������ֵΪ![]() �����������ý��������ֵΪ
�����������ý��������ֵΪ![]() ��
��
������λ�˿�ѡ���������õ�����ֵ�ϴ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һƽ����ռ��ı���![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ��ƽ�У��ҽ��ռ��ı��εı�
��ƽ�У��ҽ��ռ��ı��εı�![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��
��![]() ��
��![]() .
.
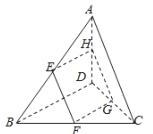
��1����֤���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
��2����![]() �DZ�
�DZ�![]() ���е㣬
���е㣬![]() ��
��![]() ������ֱ��
������ֱ��![]() ��
��![]() ���ɵĽ�Ϊ60�������߶�
���ɵĽ�Ϊ60�������߶�![]() �ij���.
�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ,
ʱ,![]() �����,��ʵ��
�����,��ʵ��![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
��2���Ƿ�ͬʱ����ʵ��![]() ��������
��������![]() ,ʹ�ú���
,ʹ�ú���![]() ��
��![]() ��ǡ��2019�����
��ǡ��2019�����![]() ������,��������з���������
������,����������������![]() ��
��![]() ��ֵ;��������,��˵������.
��ֵ;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������![]() �ķ���
�ķ���![]() ��������ͬ��ʵ������ʵ��
��������ͬ��ʵ������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪���ε����Ϊ100����������εij�������Ϊ����ʱ�����ε��ܳ���̣�����ܳ��Ƕ��٣�
��2����֪���ε��ܳ�Ϊ36����������εij�������Ϊ����ʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ������
������![]() ������
������![]() ��ɣ����е�
��ɣ����е�![]() Ϊ����
Ϊ����![]() ����Բ���ߵĽ��㣬��
����Բ���ߵĽ��㣬��![]() Ϊ����
Ϊ����![]() ����Բ���ߵĽ���.
����Բ���ߵĽ���.
������![]() ��������
��������![]() �ķ��̣�
�ķ��̣�
������ͼ����ֱ��![]() ƽ��������
ƽ��������![]() �Ľ����ߣ��������ڵ�
�Ľ����ߣ��������ڵ�![]() ����֤����
����֤����![]() ���е�
���е�![]() ��������
��������![]() ����һ���������ϣ�
����һ���������ϣ�
�����ڣ����е�����![]() ,��ֱ��
,��ֱ��![]() ����
����![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���֮�͵����ֵ.
���֮�͵����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
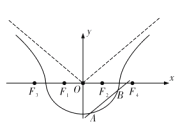
����Ŀ����˫����![]() �����ҽ���ֱ�ΪF1��F2����F1��ֱ��l��˫������֧��A��B���㣬��|BF2|��|AF2|����СֵΪ(����)
�����ҽ���ֱ�ΪF1��F2����F1��ֱ��l��˫������֧��A��B���㣬��|BF2|��|AF2|����СֵΪ(����)
A. ![]() B. 11
B. 11
C. 12 D. 16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����![]() ʱ������
ʱ������![]() �����ֵ��
�����ֵ��
��2����![]() ������
������![]() �����ֵ��
�����ֵ��
��3����֪![]() ������
������![]() �����ֵ��
�����ֵ��
��4����![]() ����
����![]() ����
����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������A1B1C1�������ڽǵ�����ֵ�ֱ������A2B2C2�������ڽǵ�����ֵ���� ��
A.��A1B1C1����A2B2C2�������������
B.��A1B1C1����A2B2C2���Ƕ۽�������
C.��A1B1C1�Ƕ۽������Σ���A2B2C2�����������
D.��A1B1C1����������Σ���A2B2C2�Ƕ۽�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com