练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么这个圆锥轴截面顶角的余弦值是    ．
    【答案】分析：设圆锥的半径为R，高为H，母线与轴所成角为θ，求出圆锥的高，利用体积相等，求出2θ的余弦值即可．
    解答：解：设圆锥的半径为R，高为H，母线与轴所成角为θ，则圆锥的高 H=R•ctgθ
    圆锥的体积 V1=πR2•H=πR3ctgθ
    半球的体积 V2=πR3
    ∵V1=V2即：πR3ctgθ=πR3
    ∴ctgθ=2
    ∴cos2θ=
    故答案为：．
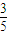
    点评：本题考查旋转体（圆柱、圆锥、圆台），棱柱、棱锥、棱台的体积，球的体积和表面积，考查计算能力，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    一个圆锥和一个半球有公共底面，如果圆锥的体积与半球的体积恰好相等，则圆锥轴截面顶角的余弦值是（　　）
    A、
    3
    4
    B、
    4
    3
    C、-
    3
    5
    D、
    3
    5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个圆锥和一个半球有公共底面，如果圆锥的体积和半球的体积相等，则这个圆锥的母线与轴所成角正弦值为（　　）
    A、
    4
    5
    B、
    3
    5
    C、
    		5
    5
    D、
    2
    		5
    5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若一个圆锥和一个半球有公共的底面，且它们的体积相等，则圆锥的轴截面的顶角是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•浦东新区二模）一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么这个圆锥轴截面顶角的余弦值是
    3
    5
    3
    5
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个圆锥和一个半球有公共底面，如果圆锥的体积和半球的体积相等，则这个圆锥的母线与轴所成角正弦值为
     
    ．

    查看答案和解析>>

    同步练习册答案