
分析 利用p∨q为真,p∧q为假,说明p,q一真一假.求出命题p:得到a≤1或a≥4.对于条件q,得到$a≥2\sqrt{2}$,然后推出a的取值范围.
解答 解:∵p∨q为真,p∧q为假,∴p,q一真一假.
由题设知,对于条件p,
∵m∈[-1,1],∴m+2∈[1,3],
∵不等式a2-5a+5≥1成立,
∴a2-5a+4≥0,解得a≤1或a≥4.
对于条件q,∵x2+ax+2=0有两个负数解,
∴$\left\{{\begin{array}{l}{△={a^2}-8≥0}\\{{x_1}+{x_2}=-a<0}\end{array}}\right.$,∴$a≥2\sqrt{2}$,…(8分)
若p真q假,则a≤1;若p假q真,则$2\sqrt{2}≤a<4$,
∴a的取值范围是:a≤1或$2\sqrt{2}≤a<4$,…(10分)
点评 本题考查命题的真假的判断,复合命题的真假,考查逻辑推理能力以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
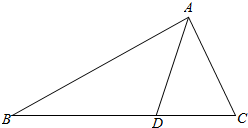 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
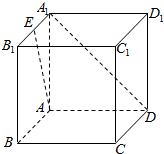 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,0)∪(0,1) | B. | [-4,0)∪(0,1] | C. | (-4,0)∪(0,1) | D. | (-∞,-4)∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com