
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点
,右焦点![]() 到右准线的距离为3.(椭圆的右准线方程为
到右准线的距离为3.(椭圆的右准线方程为![]() )
)

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.已知
两点.已知![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据题意可得![]() ,
, ![]() ,结合
,结合![]() 即可求解.
即可求解.
(2)直线l的方程为x=my+1,将直线与椭圆联立,利用弦长公式表示出|PQ|,再利用点到直线的距离求出圆心到直线![]() 的距离,结合圆
的距离,结合圆![]() 截得的弦长为
截得的弦长为![]() ,可求出m2=1,根据三角形的面积公式即可求解.
,可求出m2=1,根据三角形的面积公式即可求解.
(1)解:由题意知 ![]() ,
, ![]() ,
,
因为 ![]() ,解得a2=4,b2=3,
,解得a2=4,b2=3,
所以椭圆的方程为: ![]() 1
1
(2)解:由题意知直线l的斜率不为0,由(1)知F(1,0),
设直线l的方程为x=my+1,P(x,y),Q(x',y'),
联立直线l与椭圆的方程整理得(4+3m2)y2+6my﹣9=0,
所以y+y' ![]() ,yy'
,yy' ![]() ,
,
所以|PQ|![]() ,
,
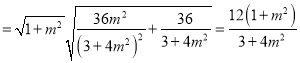 ,
,
因为圆O:x2+y2=4到l的距离d ![]() ,
,
被圆O:x2+y2=4截得的弦长为![]() ,
,
即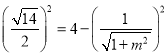
整理得14=4(4![]() ),解得m2=1,
),解得m2=1,
所以d ![]() ,|PQ|
,|PQ| ![]() ,
,
所以S△OPQ ![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2015年1月至2017年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()

A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期在8月
C. 2015年1月至12月月接待游客量的中位数为30万人
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条直线上依次有三点![]() 、
、![]() 、
、![]() .一只猎犬在点
.一只猎犬在点![]() 发现一大两小三只兔子从点
发现一大两小三只兔子从点![]() 向兔穴(点
向兔穴(点![]() )前行,立即向它们追去.当兔子发现猎犬追赶后,急忙向兔穴奔跑,大兔为了提高速度,可叼着一只小兔奔跑(速度不变,且叼起与放下小兔所耽误的时间不计).已知
)前行,立即向它们追去.当兔子发现猎犬追赶后,急忙向兔穴奔跑,大兔为了提高速度,可叼着一只小兔奔跑(速度不变,且叼起与放下小兔所耽误的时间不计).已知![]() ,
,![]() ,猎犬、大兔、小兔奔跑的速度分别为
,猎犬、大兔、小兔奔跑的速度分别为![]() 、
、![]() 、
、![]() ,兔子前行的速度为
,兔子前行的速度为![]() .则三只兔子至多在离开点
.则三只兔子至多在离开点![]() ______
______![]() 时发现猎犬,才能恰在猎犬追上自己之前全部跑进兔穴.
时发现猎犬,才能恰在猎犬追上自己之前全部跑进兔穴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
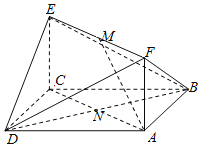
(1)求证![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)试在线段![]() 上一点
上一点![]() ,使得
,使得![]() 与
与![]() 所成的角是60°.
所成的角是60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取5人.若从这5人中随机选取3人到火车站迎接新生,求选取的3人中恰好有1名女生的概率.
附: ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题“若
”的逆否命题“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
其中错误的是__________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高血压高血糖和高血脂统称“三高”.如图是西南某地区从2010年至2016年患“三高”人数y(单位:千人)的折线图.
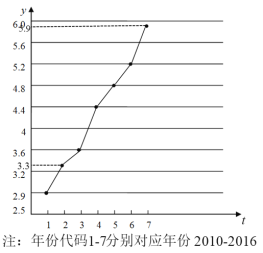
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请求出相关系数(精确到0.01)并加以说明;
的关系,请求出相关系数(精确到0.01)并加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测2018年该地区患“三高”的人数.
的回归方程,预测2018年该地区患“三高”的人数.
参考数据:![]() ,
,![]() ,
,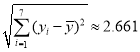 ,
,![]() .参考公式:相关系数
.参考公式:相关系数 回归方程
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: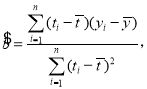
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com