Question

4．设a，b，c均为正数，且${2^a}={log_{\frac{1}{2}}}a，\;\;{（\frac{1}{2}）^b}={log_{\frac{1}{2}}}b，{（\frac{1}{2}）^c}={log_2}$c，则a，b，c由大到小的顺序为c＞b＞a．

Answer 1

分析 分别画出图象：y=2^x，$y=（\frac{1}{2}）^{x}$，y=$lo{g}_{\frac{1}{2}}x$．可得：0＜a＜b＜1.$（\frac{1}{2}）^{c}$=log₂c＞0，可得c＞1．即可得出．

解答 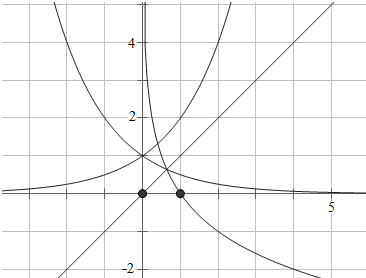解：∵${2}^{a}=lo{g}_{\frac{1}{2}}a$＞0，∴1＞a＞0；
$（\frac{1}{2}）^{b}$=$lo{g}_{\frac{1}{2}}b$＞0，1＞b＞0；
分别画出图象：y=2^x，$y=（\frac{1}{2}）^{x}$，y=$lo{g}_{\frac{1}{2}}x$．
可得：0＜a＜b＜1．
$（\frac{1}{2}）^{c}$=log₂c＞0，∴c＞1．
则a，b，c由大到小的顺序为c＞b＞a．
故答案为：c＞b＞a．

点评 本题考查了指数函数与对数函数的图象与单调性，考查了推理能力与计算能力，属于中档题．