
分析 (Ⅰ)根据函数的奇偶性求出a,b的值,从而求出函数的解析式即可;(Ⅱ)根据函数单调性的定义证明即可.
解答 解:(Ⅰ)f(x)是奇函数,
故f(-x)=$\frac{{x}^{2}+1}{-ax+b}$=-f(x)=$\frac{{x}^{2}+1}{-ax-b}$,
故b=0,
又f(1)=2,故f(1)=$\frac{2}{a}$=2,解得:a=1,
故f(x)=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$;
(Ⅱ)设x1>x2≥1,
则f(x1)-f(x2)
=(x1+$\frac{1}{{x}_{1}}$)-(x2+$\frac{1}{{x}_{2}}$)
=(x1-x2)(1-$\frac{1}{{{x}_{1}x}_{2}}$),
∵x1>x2≥1,
∴(x1-x2)>0,1-$\frac{1}{{{x}_{1}x}_{2}}$>0,
故f(x1)-f(x2)>0,f(x1)>f(x2),
故f(x)在[1,+∞)上是增函数.
点评 本题考查了函数的奇偶性问题,考查函数单调性的证明,是一道基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
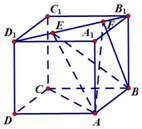 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样、分层抽样、简单随机抽样 | |
| B. | 系统抽样、系统抽样、简单随机抽样 | |
| C. | 分层抽样、简单随机抽样、简单随机抽样 | |
| D. | 系统抽样、分层抽样、简单随机抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,4} | B. | {1} | C. | {4} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com