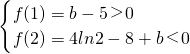解:(Ⅰ)函数f (x)的定义域为(0,+∞)…(1分)
∵f′(x)=
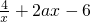
,x=2为f(x)的一个极值点…(2分)
∴f'(2)=2+4a-6=0,∴a=1.…(4分)
(Ⅱ)由(Ⅰ)知f(x)=4lnx+x
2-6x+b
∴f′(x)=
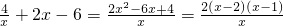
…(6分)
由f′(x)>0可得x>2或x<1,由f′(x)<0可得1<x<2.
∴函数f ( x ) 的单调递增区间为 (0,1)和 (2,+∞),单调递减区间为 (1,2 ). …(9分)
(Ⅲ) 由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.
且当x=1或x=2时,f′(x)=0. …(10分)
∴f (x) 的极大值为f(1)=4ln1+1-6+b=b-5…(11分)
f (x)的极小值为f(2)=4ln2+4-12+b=4ln2-8+b…(12分)
由题意可知
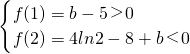
则5<b<8-4ln2…(14分)
分析:(Ⅰ)确定函数f (x)的定义域,利用x=2为f(x)的一个极值点,建立方程,可求a的值;
(Ⅱ)由(Ⅰ)知f(x)=4lnx+x
2-6x+b,求导函数,由导数的正负可得函数f(x)的单调区间;
(Ⅲ) 求出f (x) 的极大值与极小值,根据函数y=f(x)有3个不同的零点,令极大大于0.极小小于0,即可求实数b的取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查函数的零点,综合性强.

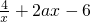 ,x=2为f(x)的一个极值点…(2分)
,x=2为f(x)的一个极值点…(2分)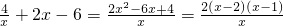 …(6分)
…(6分)