
【题目】正方体ABCD-A1B1C1D1中,二面角A-BD1-B1的大小是__________。
【答案】![]()
【解析】
设正方体ABCD﹣A1B1C1D1的棱长为1,以D为原点建立空间直角坐标系D﹣xyz,利用向量法能求出二面角A﹣BD1﹣B1的大小为![]() .
.
解:设正方体ABCD﹣A1B1C1D1的棱长为1,
以D为原点建立空间直角坐标系D﹣xyz,
A(1,0,0),B(1,1,0),D1(0,0,1),B1(1,1,1),
![]() (0,-1,0),
(0,-1,0),![]() (﹣1,﹣1,1),
(﹣1,﹣1,1),![]() (0,0,1),
(0,0,1),
设平面ABD1的法向量![]() ,
,
则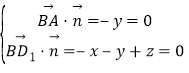 ,取x=1,得
,取x=1,得![]() (1,0,1),
(1,0,1),
设平面B1BD1的法向量![]() (a,b,c),
(a,b,c),
则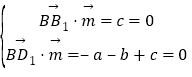 ,取a=1,得
,取a=1,得![]() (1,﹣1,0),
(1,﹣1,0),
设二面角A﹣BD1﹣B1的平面角为θ,
cosθ=﹣|cos![]() |
|![]() ,
,
∴二面角A﹣BD1﹣B1的大小为![]() .
.
故答案为:![]() .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】如图,河的两岸分别有生活小区![]() 和
和![]() ,其中
,其中![]() ,
,![]() 三点共线,
三点共线,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直线分别为
所在直线分别为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() 则河岸
则河岸![]() 可看成是曲线
可看成是曲线![]() (其中
(其中![]() 是常数)的一部分,河岸
是常数)的一部分,河岸![]() 可看成是直线
可看成是直线![]() (其中
(其中![]() 为常数)的一部分.
为常数)的一部分.

(1)求![]() 的值.
的值.
(2)现准备建一座桥![]() ,其中
,其中![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 的横坐标为
的横坐标为![]() .写出桥
.写出桥![]() 的长
的长![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并标明定义域;当
,并标明定义域;当![]() 为何值时,
为何值时,![]() 取到最小值?最小值是多少?
取到最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|x<-3,或x>5},P={x|(x-a)·(x-8)≤0}.
(1)求M∩P={x|5<x≤8}的充要条件;
(2)求实数a的一个值,使它成为M∩P={x|5<x≤8}的一个充分但不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com