
����Ŀ��ij����4̨���ͻ�������һ�����У�һ̨�����������1�ι��ϣ���ÿ̨�����Ƿ���ֹ�����������ģ����ֹ���ʱ��1�����˽���ά�ޣ�ÿ̨�������ֹ�����Ҫά�ĸ���Ϊ![]() ��
��
��1���ʸó������ж�����ά���˲��ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ĸ��ʲ�С��![]() ��
��
��2����֪1������ÿ��ֻ��ά��1̨������������ÿ����֧����ÿλ����1��Ԫ�Ĺ��ʣ�ÿ̨���������ֹ��ϻ���ֹ����ܼ�ʱά�ޣ���ʹ�ó�����5��Ԫ�������������������ó�����2�����ˣ���ó�ÿ�»����ľ�ֵ��
���𰸡���1��![]() ������2��
������2��![]() ��Ԫ��
��Ԫ��
��������
��1��һ̨���������Ƿ���ֹ��Ͽ���һ��ʵ�飬��һ�������У��������ֹ��ϵĸ���Ϊ![]() ��4̨�����൱��4�ζ����ظ����飬����ֹ��ϵĻ���̨��ΪX��
��4̨�����൱��4�ζ����ظ����飬����ֹ��ϵĻ���̨��ΪX��![]() �������Ӧ����ֵ��д���ֲ��У����㡰ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ޡ��ĸ��ʲ�����90%�Ķ�Ӧ��������
�������Ӧ����ֵ��д���ֲ��У����㡰ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ޡ��ĸ��ʲ�����90%�Ķ�Ӧ��������
��2����ó�����ΪY��Ԫ��Y�����п���ȡֵΪ18��13��8�������Ӧ�ĸ���ֵ������ֲ�������ѧ����ֵ��
��1�������������ֹ�������Ϊ�¼�![]() ����
����![]() ��
��
����ֹ��ϵĻ���̨��Ϊ![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
��ó���![]() �����ˣ�����ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά����Ϊ
�����ˣ�����ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά����Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() �������¼��ĺ��¼�����
�������¼��ĺ��¼�����
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
��Ϊ![]() ����������Ҫ3�����ˣ����ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ĸ��ʲ�С��
����������Ҫ3�����ˣ����ܱ�֤ÿ̨�������κ�ʱ��ͬʱ���ֹ���ʱ�ܼ�ʱ����ά�ĸ��ʲ�С��![]() ��
��
��2����ó�����Ϊ![]() ��Ԫ����
��Ԫ����![]() �����п���ȡֵΪ18��13��8��
�����п���ȡֵΪ18��13��8��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 18 | 13 | 8 |
|
|
|
|
����![]() ��
��
�ʸó������ľ�ֵΪ![]() ��Ԫ��
��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]()
![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ���㣬����
���㣬����![]() �ڵ�һ���ޣ�
�ڵ�һ���ޣ�![]() ����Բ��һ��.
����Բ��һ��.
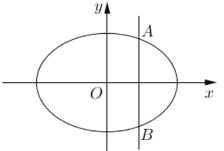
��1����![]() ��
��![]() ����Բ
����Բ![]() �����ҽ��㣬��ֱ��
�����ҽ��㣬��ֱ��![]() ��
��![]() ����
����![]() ��
��![]() �ľ����뵽ֱ��
�ľ����뵽ֱ��![]() �ľ������ʱ�����
�ľ������ʱ�����![]() �ĺ����ꣻ
�ĺ����ꣻ
��2������![]() ����
����![]() ��Գƣ���
��Գƣ���![]() ��������ʱ����ֱ��
��������ʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
��3����ֱ��![]() ��
��![]() ��
��![]() ��ֱ���
��ֱ���![]() ��֤����
��֤����![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ|2x-1|+|2x-2|��x+3�Ľ⼯��A��
������A��
������x��y��A��������a��R����֤��xy��||x+a|-|y+a||����x2+y2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��ͼ����
��ͼ����![]() ��ȡ�ü�ֵ4.
��ȡ�ü�ֵ4.
��1������![]() �ĵ������䣻
�ĵ������䣻
��2�����ں���![]() ��������������������
��������������������![]() ��
��![]() ����
����![]() ʱ������
ʱ������![]() ��ֵ����
��ֵ����![]() ���������
���������![]() ���
�к���![]() �ġ�����ֵ���䡱.�ʺ���
�ġ�����ֵ���䡱.�ʺ���![]() �Ƿ���ڡ�����ֵ���䡱�������ڣ�������еġ�����ֵ���䡱���������ڣ���˵������.
�Ƿ���ڡ�����ֵ���䡱�������ڣ�������еġ�����ֵ���䡱���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������13�֣�
��ͼ����֪������![]() ������
������![]() ����һֱ����
����һֱ����![]() �ཻ��
�ཻ��![]() ���㣬����
���㣬����![]() ��
��![]() ���ƽ������ֱ��
���ƽ������ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() Ϊ����ԭ�㣩.
Ϊ����ԭ�㣩.

(1)֤��������![]() �ڶ�ֱ���ϣ�
�ڶ�ֱ���ϣ�
(2)��![]() ������һ������
������һ������![]() ������
������![]() �ᣩ��ֱ��
�ᣩ��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���루1���еĶ�ֱ���ཻ�ڵ�
���루1���еĶ�ֱ���ཻ�ڵ�![]() ��֤����
��֤����![]() Ϊ��ֵ������˶�ֵ.
Ϊ��ֵ������˶�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֳ��ģ����������ֳ���飬ij�����̼ҵĺ���Ʒÿֻ�������ˣ������������·�����̬�ֲ�![]() ��
��
��1���������10ֻ���̼ҵĺ���Ʒ����������һֻ����С��![]() �˸ú���Ʒ�ĸ��ʣ�
�˸ú���Ʒ�ĸ��ʣ�
��2��2020����̼ҿ��������Ƚ���ֳ����Ͷ�룬���̼���Ԥ���Ƚ���ֳ����Ͷ��Ϊ49ǧԪʱ�������������������������Ƚ���ֳ����Ͷ��![]() ��ǧԪ��������������
��ǧԪ��������������![]() ��ǧԪ����
��ǧԪ����![]() �������ݻ���ɢ��ͼ����ɢ��ͼ��������ֲ���������Ϊ�����㼯��������
�������ݻ���ɢ��ͼ����ɢ��ͼ��������ֲ���������Ϊ�����㼯��������![]() �ĸ�������
�ĸ�������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
�� ![]() ������
������![]() ��
��![]() =
=![]()
![]() ������������ͳ��������
������������ͳ��������![]() ����
����![]() �Ļع鷽�̣���Ԥ���Ƚ���ֳ����Ͷ��Ϊ49ǧԪʱ��������������
�Ļع鷽�̣���Ԥ���Ƚ���ֳ����Ͷ��Ϊ49ǧԪʱ��������������
�������������![]() ����
����![]() ��
��![]() ��
��
����һ������![]() ��
��![]() ��
��![]() ��
��![]() ����ع���
����ع���![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ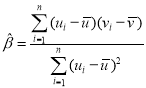 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�Բ
�У�Բ![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ���ڵ�
���ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1�����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2����![]() ��ֱ����
��ֱ����![]() ����
����![]() ��
��![]() ���㣬���߶�
���㣬���߶�![]() ���е�Ϊ
���е�Ϊ![]() ����
����![]() �����ı���
�����ı���![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����x��R����f��x��+2f����x����mx��6����f��x����lnx���������ʵ��m��ȡֵ��Χ��_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ԭ��Ϊ���㣬![]() ��Ǹ�����Ϊ���ᣬ���ȵ�λ��ͬ������������ϵ������
��Ǹ�����Ϊ���ᣬ���ȵ�λ��ͬ������������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() ����
����![]() ����б��Ϊ
����б��Ϊ![]() .
.
��1��������![]() �ļ����귽�̻�Ϊֱ�����귽�̣�д��ֱ��
�ļ����귽�̻�Ϊֱ�����귽�̣�д��ֱ��![]() �IJ������̵ı���ʽ��
�IJ������̵ı���ʽ��
��2����ֱ֪��![]() ������
������![]() ��
��![]() ���㣬��
���㣬��![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com