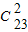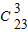将(x+y+z)5展开合并同类项后共有 项,其中x3yz项的系数是 .
【答案】
分析:将(x+y+z)
5展开合并同类项后,每一项都是 m•x
a•y
b•z
c 的形式,且a+b+c=5,其中,m是实数,a、b、c∈N.利用组合模型求解该问题,恰当构造分组模型,
利用组合法解决该问题.
把(x+y+z)
5 的展开式看成5个因式(x+y+z)的乘积形式.从中任意选3个因式,这3个因式都取x,另外的2个因式分别取y、z,相乘即得含x
3yz项,由此求得含x
3yz项的系数.
解答:解:将(x+y+z)
5展开合并同类项后,每一项都是 m•x
a•y
b•z
c 的形式,且a+b+c=5,其中,m是实数,a、b、c∈N,
构造8个完全一样的小球模型,分成3组,每组至少一个,共有分法

种,
每一组中都去掉一个小球的数目分别作为(x+y+z)
5的展开式中每一项中x,y,z各字母的次数,
小球分组模型与各项的次数是一一对应的.
故 将(x+y+z)
5展开合并同类项后共有
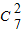
=21项.
把(x+y+z)
5 的展开式看成5个因式(x+y+z)的乘积形式.
从中任意选3个因式,这3个因式都取x,另外的2个因式分别取y、z,相乘即得含x
3yz项,故含x
3yz项的系数为
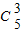
=20,
故答案为 21;20.
点评:本题主要考查了二项式定理的应用,二项展开式的系数特征,考查构造法解决该问题,关键要构造一个适当的组合模型,属于中档题.

 种,
种,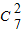 =21项.
=21项.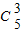 =20,
=20,