
某市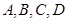 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 | 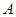 |  | 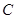 | 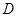 |
| 人数 | 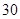 | 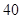 | 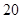 | 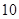 |
 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?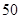 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;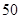 名学生中,从自
名学生中,从自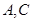 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学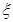 表示抽得
表示抽得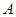 中学的学生人数,求
中学的学生人数,求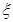 的分布列和期望.
的分布列和期望. (1) 从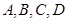 四所中学抽取的学生人数分别为
四所中学抽取的学生人数分别为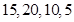 ;(2) 这两名学生自同一所中学的概率为
;(2) 这两名学生自同一所中学的概率为 ,(3)
,(3)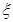 的分布列为:
的分布列为: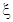

1 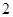
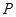

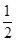
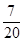
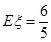 .
.
解析试题分析:(1) 由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100名,抽取的样本容量与总体个数的比值为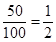 .据此即可计算出答案;(2) 利用组合的意义分别计算出从参加问卷调查的50名学生中随机抽取两名学生的方法和这两名学生来自同一所中学的取法,再利用古典概型的概率计算公式即可得出;(3)由(1) 知,在参加问卷调查的50名学生中,来自A,C两所中学的学生人数分别为15,10.可得ξ的可能取值为0,1,2.利用超几何分布的概率计算公式
.据此即可计算出答案;(2) 利用组合的意义分别计算出从参加问卷调查的50名学生中随机抽取两名学生的方法和这两名学生来自同一所中学的取法,再利用古典概型的概率计算公式即可得出;(3)由(1) 知,在参加问卷调查的50名学生中,来自A,C两所中学的学生人数分别为15,10.可得ξ的可能取值为0,1,2.利用超几何分布的概率计算公式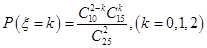 ,即可得到分布列,利用数学期望的概率计算公式即可得出.
,即可得到分布列,利用数学期望的概率计算公式即可得出.
试题解析:(1) 由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100名,
抽取的样本容量与总体个数的比值为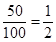 .
.
∴应从 四所中学抽取的学生人数分别为
四所中学抽取的学生人数分别为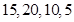 . 4分
. 4分
(2) (2) 设“从参加问卷调查的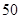 名学生中随机抽取两名学生,求这两名学生自同一所中学”为事件
名学生中随机抽取两名学生,求这两名学生自同一所中学”为事件 ,从参加问卷调查的
,从参加问卷调查的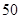 名学生中随机抽取两名学生随机抽取两名学生的取法有
名学生中随机抽取两名学生随机抽取两名学生的取法有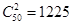 种,这两名学生来自同一所中学的取法有
种,这两名学生来自同一所中学的取法有 ,所以
,所以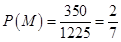 .从参加问卷调查的
.从参加问卷调查的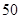 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率 ; 7分
; 7分
(3)由(1)知,在参加问卷调查的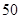 名学生中,自
名学生中,自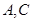 两所中学的学生人数分别
两所中学的学生人数分别
为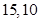 .
.
依题意得,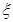 的可能取值为
的可能取值为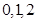 , 8分
, 8分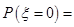

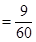 ,
, 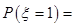

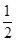 ,
,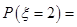
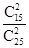
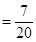 . 11分
. 11分
∴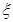 的分布列为:
的分布列为: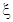

1 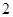
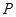

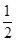
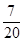
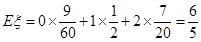 12分
12分
考点:离散型随机变量及其分布列;等可能事件的概率.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 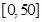 | 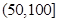 | 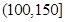 | 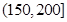 | 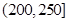 | 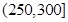 | 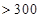 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
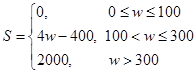 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率; 列联表,并判断能否有
列联表,并判断能否有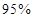 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?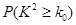 | 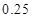 | 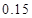 | 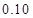 | 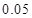 | 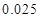 | 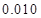 | 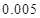 | 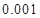 |
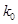 | 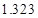 | 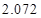 | 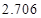 | 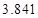 | 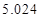 | 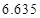 | 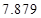 | 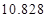 |
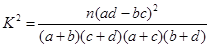
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是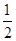 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两名同学参加“汉字听写大赛”选拔测试,在相同测试条件下,两人5次测试的成绩(单位:分)如下表: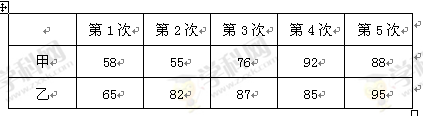
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,设抽到的两个成绩中,90分以上的个数为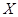 ,求随机变量
,求随机变量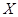 的分布列和期望
的分布列和期望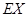 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出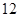 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 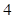 | 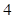 | 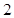 | 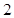 |
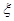 ,求随机变量
,求随机变量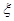 的分布列及数学期望
的分布列及数学期望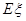 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据民生所望,相关部门对所属服务单位进行整治行核查,规定:从甲类3个指标项中随机抽取2项,从乙类2个指标项中随机抽取1项.在所抽查的3个指标项中,3项都优秀的奖励10万元;只有甲类2项优秀的奖励6万元;甲类只有1项优秀、乙类1项优秀的提出警告,有2项或2项以上不优秀的停业运营并罚款8万元.已知某家服务单位甲类3项指标项中有2项优秀,乙类2项指标项中有1项优秀.
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.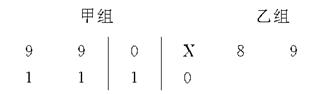
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2=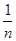 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com