
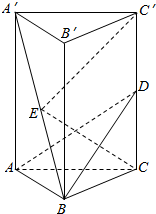
 如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证:
如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证:分析 (1)取AB中点O,连接OE、OD,证明四边形EODC'为平行四边形,可得C'E∥OD,即可证明直线EC′∥平面ABD;
(2)连接OC、DE,证明EC⊥OD,AB⊥EC,即可证明直线EC⊥平面ABD.
解答 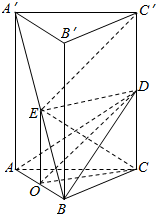 证明:(1)取AB中点O,连接OE、OD.
证明:(1)取AB中点O,连接OE、OD.
∵E、O为A'B,AB中点,∴OE平行且等于$\frac{1}{2}$AA′
又∵C′D平行且等于$\frac{1}{2}$CC′
∴OE平行且等于C′D,
∴四边形EODC'为平行四边形,∴C'E∥OD
又∵OD?面ABD,C'E?面ABD,
∴C'E∥面ABD…(6分)
(2)连接OC、DE
∵三棱柱ABC-A'B'C'为正三棱柱,
∴AA'⊥面ABC,
∴EO⊥面ABC
∵AB,OC?面ABC,
∴EO⊥AB,EO⊥OC
∵$EO=\frac{1}{2}CC'=\frac{{\sqrt{3}}}{2}BC=OC$,
∴四边形EOCD为正方形,∴EC⊥OD
又∵CA=CB,∴AB⊥OC
∵EO、OC是平面EOCC'内的相交直线,∴AB⊥面EOCC'
∵EC?面EOCC',∴AB⊥EC
∵AB、OD是平面ABD内的相交直线,
∴直线EC⊥平面ABD…(14分)
点评 本题考查线面平行、垂直的判定,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
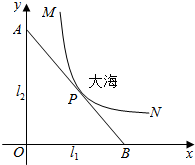 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com