
已知函数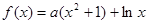 .
.
(Ⅰ)讨论函数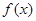 的单调性;
的单调性;
(Ⅱ)若对任意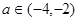 及
及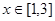 时,恒有
时,恒有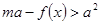 成立,求实数
成立,求实数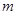 的取值范围.
的取值范围.
 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:解答题
已知函数 ,其中
,其中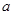 为大于零的常数,
为大于零的常数,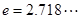 ,函数
,函数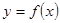 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为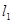 ,函数
,函数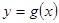 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为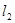 ,且
,且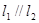 .
.
(I)若在闭区间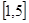 上存在
上存在 使不等式
使不等式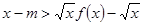 成立,求实数
成立,求实数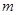 的取值范围;
的取值范围;
(II)对于函数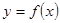 和
和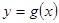 公共定义域内的任意实数
公共定义域内的任意实数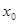 ,我们把
,我们把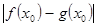 的值称为两函数在
的值称为两函数在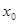 处的偏差.求证:函数
处的偏差.求证:函数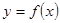 和
和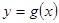 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为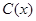 ,当年产量不足80千件时,
,当年产量不足80千件时,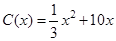 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,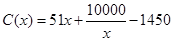 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润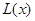 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果函数f(x)的定义域为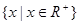 ,且f(x)为增函数,f(xy)=f(x)+f(y)。
,且f(x)为增函数,f(xy)=f(x)+f(y)。
(1)证明: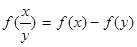 ;
;
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时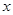 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米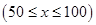 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油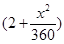 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(Ⅰ)求这次行车总费用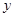 关于
关于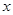 的表达式;
的表达式;
(Ⅱ)当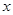 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场准备在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电商品、4种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种日用商品的概率;
(Ⅱ)商场对选出的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高90元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等可能的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).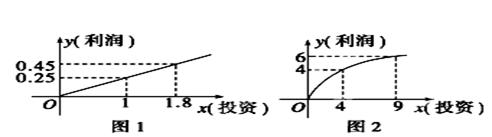
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com