Question

9．已知圆O：x²+y²=a²（a＞0），点A（0，4），B（2，2）．
（1）若线段AB的中垂线与圆O相切，求实数a的值；
（2）过直线AB上的点P引圆O的两条切线，切点为M，N，若∠MPN=60°，则称点P为“好点”．若直线AB上有且只有两个“好点”，求实数a的取值范围．

Answer 1

分析 （1）求出AB的中点坐标为（1，3），求出直线AB的斜率，AB的中垂线方程x-y+2=0，利用直线与圆相切，求解a即可．
（2）连接PO，OM，得到圆O'的方程为x²+y²=4a²，直线AB上有且只有两个“好点”，推出圆心O到直线AB的距离$\frac{4}{{\sqrt{2}}}＜2a$，求解即可．

解答 解：（1）由A（0，4），B（2，2）得AB的中点坐标为（1，3），直线AB的斜率为-1，…..（2分）
所以AB的中垂线方程为y-3=1×（x-1），即x-y+2=0，…..（4分）
又因为AB的中垂线与圆O相切，
所以圆心O到AB中垂线的距离$\frac{2}{{\sqrt{2}}}=a$，即$a=\sqrt{2}$．…（6分）
（2）连接PO，OM，
在Rt△POM中，∠OPM=30°，OM=a，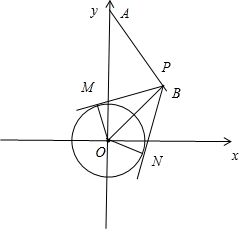
所以PO=2OM=2a，…．（8分）
所以点P的轨迹是以O为圆心，2a为半径的圆，记为圆O'，
则圆O'的方程为x²+y²=4a²，…..（10分）
又因为直线AB的方程为x+y-4=0，且直线AB上有且只有两个“好点”，
则直线AB与圆O'相交，所以圆心O到直线AB的距离$\frac{4}{{\sqrt{2}}}＜2a$，
故实数a的取值范围是$（\sqrt{2}，+∞）$．…．（14分）

点评 本题考查直线与圆的位置关系的综合应用，圆的方程的求法，考查转化思想以及计算能力．