
【题目】已知抛物线![]() 上横坐标为
上横坐标为![]() 的点到焦点的距离为
的点到焦点的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 的直线与抛物线交于不同的两点
的直线与抛物线交于不同的两点![]() ,且以
,且以![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,求
,求![]() 的面积。
的面积。
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证:对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ;
;
(Ⅲ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个线性回归方程![]() ,变量x增加1个单位时,y平均增加5个单位;
,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量x,y的相关系数为r,则|r|越接近于0,x和y之间的线性相关程度越强;
④在一个2×2列联表中,由计算得K2的值,则K2的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中重要的一部分,其中大学生更是频频使用网络外卖服务.![]() 市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了
市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了![]() 人,并将这
人,并将这![]() 人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过
人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过![]() 元):
元):
消费金额(单位:百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
![]() 由频数分布表可以认为,该市大学生网络外卖消费金额
由频数分布表可以认为,该市大学生网络外卖消费金额![]() (单位:元)近似地服从正态分布
(单位:元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值,
(每组数据取区间的中点值,![]() ).现从该市任取
).现从该市任取![]() 名大学生,记其中网络外卖消费金额恰在
名大学生,记其中网络外卖消费金额恰在![]() 元至
元至![]() 元之间的人数为
元之间的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
![]()
![]() 市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值
市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值![]() 元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第
元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第![]() 格、第
格、第![]() 格、第
格、第![]() 格、…、第
格、…、第![]() 格共
格共![]() 个方格.棋子开始在第
个方格.棋子开始在第![]() 格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是
格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是![]() ,其中
,其中![]() ),若掷出正面,将棋子向前移动一格(从
),若掷出正面,将棋子向前移动一格(从![]() 到
到![]() ),若掷出反面,则将棋子向前移动两格(从
),若掷出反面,则将棋子向前移动两格(从![]() 到
到![]() ).重复多次,若这枚棋子最终停在第
).重复多次,若这枚棋子最终停在第![]() 格,则认为“闯关成功”,并赠送
格,则认为“闯关成功”,并赠送![]() 元充值饭卡;若这枚棋子最终停在第
元充值饭卡;若这枚棋子最终停在第![]() 格,则认为“闯关失败”,不再获得其他奖励,活动结束.
格,则认为“闯关失败”,不再获得其他奖励,活动结束.
①设棋子移到第![]() 格的概率为
格的概率为![]() ,求证:当
,求证:当![]() 时,
时,![]() 是等比数列;
是等比数列;
②若某大学生参与这档“闯关游戏”,试比较该大学生闯关成功与闯关失败的概率大小,并说明理由.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查,随机抽查了200人,将他们的月收入(单位:百元)频数分布及超前消费的认同人数整理得到如下表格:
月收入(百元) |
|
|
|
|
|
|
频数 | 20 | 40 | 60 | 40 | 20 | 20 |
认同超前消费的人数 | 8 | 16 | 28 | 21 | 13 | 16 |
(1)根据以上统计数据填写下面![]() 列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
月收入不低于8000元 | 月收入低于8000元 | 总计 | |
认同 | |||
不认同 | |||
总计 |
(2)若从月收入在![]() 的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
参考公式: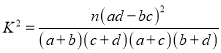 (其中
(其中![]() ).
).
附表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com