Question

试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。

 

Answer 1

【答案】

840与1764的最大公约数就是84，440与556的最大公约数是4

【解析】(1)辗转相除法:用较大的数字除以较小的数字，得到商和余数，然后再用上一式

中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约

数．

(2) 用更相减损术求440与556的最大公约数，先用大数减去小数，再用减数和差中较大的

数字减去较小的数字，这样减下去，知道减数和差相同，得到最大公约数．

解：（1）用辗转相除法求840与1764的最大公约数。

1764=840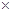2+84，840=84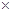10+0，

所以840与1764的最大公约数就是84。

(2）用更相减损术求440与556的最大公约数。

 556-440=116，440-116=324，324-116=208，208-116=92，116-92=24，92-24=68，

68-24=44，44-24=20，24-20=4，20-4=16，16-4=12，12-4=8，8-4=4。

440与556的最大公约数是4。