
【题目】甲、乙两名射击运动员一次射击命中目标的概率分别是0.7,0.6,且每次射击命中与否相互之间没有影响,求:
(1)甲射击三次,第三次才命中目标的概率;
(2)甲、乙两人在第一次射击中至少有一人命中目标的概率;
(3)甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率.
【答案】(1)![]() ;(2)0.88;(3)
;(2)0.88;(3)![]() .
.
【解析】
(1)“甲第三次才命中目标”为事件![]() ,且三次射击相互独立,利用独立重复试验概率计算公式即可求得答案;
,且三次射击相互独立,利用独立重复试验概率计算公式即可求得答案;
(2)求该事件的反面的概率,用1减其即可;
(3)设“甲在两次射击命中目标i次”为事件![]() ,“乙在两次射击命中目标i次”为事件
,“乙在两次射击命中目标i次”为事件![]() ,则事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为
,则事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为![]() ,用独立重复试验概率计算公式即可求得答案.
,用独立重复试验概率计算公式即可求得答案.
记“甲第i次射击命中目标”为事件![]() ,“乙第i次射击命中目标”为事件
,“乙第i次射击命中目标”为事件![]() ,依题意得
,依题意得![]() ,
,![]() ,且
,且![]() ,
,![]() (
(![]() )相互独立.
)相互独立.
(1)“甲第三次才命中目标”为事件![]() ,且三次射击相互独立,
,且三次射击相互独立,
![]() .
.
答:甲第三次才命中目标的概率为![]() .
.
(2)“甲、乙两人在第一次射击中至少有一人命中目标”为事件C.
![]() .
.
答:甲、乙两人在第一次射击中至少有一人命中目标的概率为0.88.
(3)设“甲在两次射击命中目标i次”为事件![]() ,
,
“乙在两次射击命中目标i次”为事件![]() ,
,
![]() 事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为
事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为![]() ,且
,且![]() ,
,![]() 为互斥事件,
为互斥事件,
![]() 所求的概率为
所求的概率为![]()
![]()
![]()
答:甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,平面
中,底面ABCD为正方形,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,E,F分别为AD,PB的中点.
,E,F分别为AD,PB的中点.
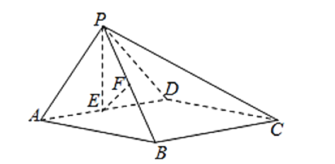
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求证:![]() 平面PCD;
平面PCD;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国际山地旅游大会于10月14日在贵州召开,据统计有来自全世界的4000名女性和6000名男性徒步爱好者参与徒步运动,其中抵达终点的女性与男性徒步爱好者分别为1000名和2000名,抵达终点的徒步爱好者可获得纪念品一份。若记者随机电话采访参与本次徒步运动的1名女性和1名男性徒步爱好者,其中恰好有1名徒步爱好者获得纪念品的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是梯形,AB//CD,DA⊥AB,BC⊥SC,SA=AD=3,AB=6,点E在棱SD上,且VS-ACE=2VE-ACD。

(1)求证:BC⊥平面SAC;
(2)求二面角S-AE-C的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众.
.某机构就《流浪地球》是否好看的问题随机采访了4名观众.
(1)若这4名观众2男2女,求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)若这4名观众都是男性,设X表示这4名观众中认为《流浪地球》好看的人数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
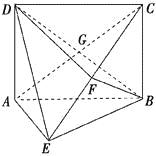
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与![]() 的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与![]() 的浓度的数据如下表:
的浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 100 | 102 | 108 | 114 | 116 |
| 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若周六同一时间段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时![]() 的浓度为多少.
的浓度为多少.
参考公式: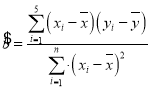 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
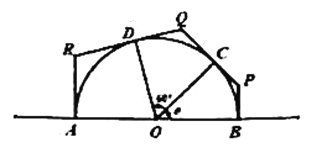
【题目】为美化城市环境,相关部门需对一半圆形中心广场进行改造出新,为保障市民安全,施工队对广场进行围挡施工.如图,围挡经过直径的两端点A,B及圆周上两点C,D围成一个多边形ABPQR,其中AR,RQ,QP,PB分别与半圆相切于点A,D,C,B.已知该半圆半径OA长30米,∠COD为60°,设∠BOC为![]() .
.
(1)求围挡内部四边形OCQD的面积;
(2)为减少对市民出行的影响,围挡部分面积要尽可能小.求该围挡内部多边形ABPQR面积的最小值?并写出此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com