
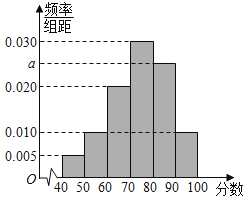
ΓΨΧβΡΩΓΩΈΣ”≠Ϋ”2022Ρξ±±Ψ©Ε§ΦΨΑ¬‘ΥΜαΘ§Τ’ΦΑΕ§Α¬÷Σ ΕΘ§Ρ≥–ΘΩΣ’ΙΝΥΓΑ±υ―©¥πΧβΆθΓ±Ε§Α¬÷Σ ΕΨΚ»ϋΜνΕ·.œ÷¥”≤ΈΦ”Ε§Α¬÷Σ ΕΨΚ»ϋΜνΕ·ΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ100Οϊ―ß…ζΘ§ΫΪΥϊΟ«ΒΡ±»»ϋ≥…Φ®Θ®¬ζΖ÷ΈΣ100Ζ÷Θ©Θ§Ζ÷ΈΣ6ΉιΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ®1Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©Φ«![]() ±μ Ψ ¬ΦΰΓΑ¥”≤ΈΦ”Ε§Α¬÷Σ ΕΨΚ»ϋΜνΕ·ΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ“ΜΟϊ―ß…ζΘ§ΗΟ―ß…ζΒΡ±»»ϋ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷Γ±Θ§ΙάΦΤ
±μ Ψ ¬ΦΰΓΑ¥”≤ΈΦ”Ε§Α¬÷Σ ΕΨΚ»ϋΜνΕ·ΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ“ΜΟϊ―ß…ζΘ§ΗΟ―ß…ζΒΡ±»»ϋ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷Γ±Θ§ΙάΦΤ![]() ΒΡΗ≈¬ ΘΜ
ΒΡΗ≈¬ ΘΜ
Θ®3Θ©‘Ύ≥ι»ΓΒΡ100Οϊ―ß…ζ÷–Θ§ΙφΕ®ΘΚ±»»ϋ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΈΣΓΑ”≈–ψΓ±Γ·Θ§±»»ϋ≥…Φ®ΒΆ”Ύ80Ζ÷ΈΣΓΑΖ«”≈–ψΓ±.«κΫΪœ¬ΟφΒΡ![]() Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤Δ≈–Εœ «Ζώ”–99.9%ΒΡΑ―Έ’»œΈΣΓΑ±»»ϋ≥…Φ® «Ζώ”≈–ψ”κ–‘±π”–ΙΊΓ±?
Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤Δ≈–Εœ «Ζώ”–99.9%ΒΡΑ―Έ’»œΈΣΓΑ±»»ϋ≥…Φ® «Ζώ”≈–ψ”κ–‘±π”–ΙΊΓ±?
”≈–ψ | Ζ«”≈–ψ | ΚœΦΤ | |
Ρ–…ζ | 40 | ||
≈°…ζ | 50 | ||
ΚœΦΤ | 100 |
≤ΈΩΦΙΪ ΫΦΑ ΐΨίΘΚ![]() Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©Ν–ΝΣ±μΦϊΫβΈωΘ§ΟΜ”–
ΘΜΘ®3Θ©Ν–ΝΣ±μΦϊΫβΈωΘ§ΟΜ”–
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Χβ“βΫαΚœΗςΉιΤΒ¬ ΚΆΈΣ1Φ¥Ω…ΒΟΫβΘΜ
Θ®2Θ©”…Χβ“β«σ≥ω±»»ϋ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΒΡΤΒ¬ Θ§”…―υ±ΨΙάΦΤΉήΧεΦ¥Ω…ΒΟΫβΘΜ
Θ®3Θ©”…Χβ“βΆξ≥…Ν–ΝΣ±μΘ§¥ζ»κΙΪ Ϋ«σ≥ω![]() Θ§”κ
Θ§”κ![]() ±»ΫœΚσΦ¥Ω…ΒΟΫβ.
±»ΫœΚσΦ¥Ω…ΒΟΫβ.
Θ®1Θ©”…Χβ“β![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
Θ®2Θ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…ΒΟ―υ±Ψ÷–±»»ϋ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΒΡΤΒ¬ ΈΣΘΚ![]() Θ§
Θ§
ΓύΩ…ΙάΦΤ![]() ΒΡΗ≈¬ ΈΣ0.35ΘΜ
ΒΡΗ≈¬ ΈΣ0.35ΘΜ
Θ®3Θ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…÷Σ≥ι»ΓΒΡ100Οϊ―ß…ζ÷–Θ§”≈–ψΒΡ»Υ ΐΈΣ![]() Θ§
Θ§
Ν–ΝΣ±μ»γœ¬ΘΚ
”≈–ψ | Ζ«”≈–ψ | ΚœΦΤ | |
Ρ–…ζ | 10 | 40 | 50 |
≈°…ζ | 25 | 25 | 50 |
ΚœΦΤ | 35 | 65 | 100 |
Γύ![]() Θ§
Θ§
Γύ≤ΜΡή”–![]() ΒΡΑ―Έ’»œΈΣ±»»ϋ≥…Φ® «Ζώ”≈–ψ”κ–‘±π”–ΙΊ.
ΒΡΑ―Έ’»œΈΣ±»»ϋ≥…Φ® «Ζώ”≈–ψ”κ–‘±π”–ΙΊ.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΘΚ
ΘΚ![]() ΒΡ”“ΫΙΒψΈΣ
ΒΡ”“ΫΙΒψΈΣ![]() Θ§…œΕΞΒψΈΣ
Θ§…œΕΞΒψΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§«“‘≠ΒψΒΫ÷±œΏ
Θ§«“‘≠ΒψΒΫ÷±œΏ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©»τ≤ΜΨ≠ΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ΘΚ
ΘΚ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§«“”κ‘≤
ΝΫΒψΘ§«“”κ‘≤![]() œύ«–. ‘ΧΫΨΩ
œύ«–. ‘ΧΫΨΩ![]() ΒΡ÷ή≥Λ «ΖώΈΣΕ®÷ΒΘ§»τ «Θ§«σ≥ωΕ®÷ΒΘΜ»τ≤Μ «Θ§«κΥΒΟςάμ”….
ΒΡ÷ή≥Λ «ΖώΈΣΕ®÷ΒΘ§»τ «Θ§«σ≥ωΕ®÷ΒΘΜ»τ≤Μ «Θ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆ®ΙΐΥφΜζ―·Έ ![]() Οϊ≤ΜΆ§–‘±πΒΡ¥σ―ß…ζ «ΖώΑ°ΚΟΡ≥œν‘ΥΕ·Θ§ΒΟΒΫ»γœ¬ΒΡ
Οϊ≤ΜΆ§–‘±πΒΡ¥σ―ß…ζ «ΖώΑ°ΚΟΡ≥œν‘ΥΕ·Θ§ΒΟΒΫ»γœ¬ΒΡ![]() Ν–ΝΣ±μΘΚ
Ν–ΝΣ±μΘΚ
Ρ– | ≈° | |
Α°ΚΟ | 40 | 20 |
≤ΜΑ°ΚΟ | 20 | 30 |
”…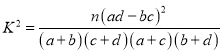 ΥψΒΟ
ΥψΒΟ![]() Θ§
Θ§
≤Έ’’ΗΫ±μΘ§“‘œ¬≤Μ’ΐ»ΖΒΡ”–Θ® Θ©
ΗΫ±μΘΚ
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬Θ§»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
ΒΡ«ΑΧαœ¬Θ§»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
B.‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬Θ§»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
ΒΡ«ΑΧαœ¬Θ§»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
C.”–![]() “‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±π”–ΙΊΓ±
D.”–![]() “‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
“‘…œΒΡΑ―Έ’»œΈΣΓΑΑ°ΚΟΗΟœν‘ΥΕ·”κ–‘±πΈόΙΊΓ±
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«σ‘ΎΆΦΥυ ΨΒΡ![]() ΒΡΖΫΗώ÷–ΓΑ»ΠΓ±ΒΡΗω ΐ.‘Ύ’βάοΘ§“ΜΧθΖβ±’ΒΡ’έœΏΫ–Ήω»ΠΘ§»γΙϊ’βΧθ’έœΏΒΡ±ΏΨυ”…ΖΫΗώΒΡ±ΏΉι≥…Θ§«“’έœΏΨ≠ΙΐΒΡ»Έ“β“ΜΗωΖΫΗώΕΞΒψΕΦ÷Μ”κ’έœΏΒΡΝΫΧθ±ΏœύΝ§.
ΒΡΖΫΗώ÷–ΓΑ»ΠΓ±ΒΡΗω ΐ.‘Ύ’βάοΘ§“ΜΧθΖβ±’ΒΡ’έœΏΫ–Ήω»ΠΘ§»γΙϊ’βΧθ’έœΏΒΡ±ΏΨυ”…ΖΫΗώΒΡ±ΏΉι≥…Θ§«“’έœΏΨ≠ΙΐΒΡ»Έ“β“ΜΗωΖΫΗώΕΞΒψΕΦ÷Μ”κ’έœΏΒΡΝΫΧθ±ΏœύΝ§.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ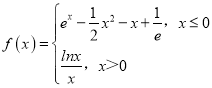 Θ§»τΖΫ≥ΧfΘ®xΘ©©¹m=0«Γ”–ΝΫΗω ΒΗυΘ§‘ρ Β ΐmΒΡ»Γ÷ΒΖΕΈß «_____.
Θ§»τΖΫ≥ΧfΘ®xΘ©©¹m=0«Γ”–ΝΫΗω ΒΗυΘ§‘ρ Β ΐmΒΡ»Γ÷ΒΖΕΈß «_____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() Θ§Βψ
Θ§Βψ![]() Θ§
Θ§![]() «‘≤
«‘≤![]() …œ»Έ“β“ΜΒψΘ§œΏΕΈ
…œ»Έ“β“ΜΒψΘ§œΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Β±Βψ
Θ§Β±Βψ![]() ‘Ύ‘≤…œ‘ΥΕ· ±Θ§Βψ
‘Ύ‘≤…œ‘ΥΕ· ±Θ§Βψ![]() ΒΡΙλΦΘΈΣ«ζœΏ
ΒΡΙλΦΘΈΣ«ζœΏ![]() Θ°
Θ°
![]() 1
1![]() «σ«ζœΏ
«σ«ζœΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
![]() 2
2![]() »τ÷±œΏ
»τ÷±œΏ![]()
![]() ”κ«ζœΏ
”κ«ζœΏ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΝΫΒψΘ§
ΝΫΒψΘ§![]() ΈΣΉχ±ξ‘≠ΒψΘ§«σ
ΈΣΉχ±ξ‘≠ΒψΘ§«σ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘ°
ΟφΜΐΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΥΡάβΉΕ![]() ΒΡΒΉΟφ «±Ώ≥ΛΈΣ
ΒΡΒΉΟφ «±Ώ≥ΛΈΣ![]() ΒΡΝβ–ΈΘ§
ΒΡΝβ–ΈΘ§![]() Θ§ΒψE «άβBCΒΡ÷–ΒψΘ§
Θ§ΒψE «άβBCΒΡ÷–ΒψΘ§![]() Θ§ΒψP‘ΎΤΫΟφABCDΒΡ…δ”ΑΈΣOΘ§FΈΣάβPA…œ“ΜΒψΘ°
Θ§ΒψP‘ΎΤΫΟφABCDΒΡ…δ”ΑΈΣOΘ§FΈΣάβPA…œ“ΜΒψΘ°

![]() 1
1![]() «σ÷ΛΘΚΤΫΟφ
«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφBCFΘΜ
ΤΫΟφBCFΘΜ
![]() 2
2![]() »τ
»τ![]() ΤΫΟφPDEΘ§
ΤΫΟφPDEΘ§![]() Θ§«σΥΡάβΉΕ
Θ§«σΥΡάβΉΕ![]() ΒΡΧεΜΐΘ°
ΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§÷±œΏ
÷–Θ§÷±œΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§÷±œΏ
ΈΣ≤Έ ΐΘ©Θ§÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΤΫ––Θ§«“ΙΐΉχ±ξ‘≠ΒψΘ§‘≤
ΤΫ––Θ§«“ΙΐΉχ±ξ‘≠ΒψΘ§‘≤![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ°“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§
ΈΣ≤Έ ΐΘ©Θ°“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
Θ®1Θ©«σ÷±œΏ![]() ΚΆ‘≤
ΚΆ‘≤![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©…η÷±œΏ![]() ΚΆ‘≤
ΚΆ‘≤![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() ΒΡ÷ή≥ΛΘ°
ΒΡ÷ή≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ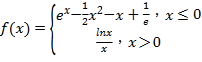 Θ§»τΖΫ≥ΧfΘ®xΘ©©¹m=0«Γ”–ΝΫΗω ΒΗυΘ§‘ρ Β ΐmΒΡ»Γ÷ΒΖΕΈß «_____.
Θ§»τΖΫ≥ΧfΘ®xΘ©©¹m=0«Γ”–ΝΫΗω ΒΗυΘ§‘ρ Β ΐmΒΡ»Γ÷ΒΖΕΈß «_____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com