
【题目】“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某市交通管理部门于某天晚上8点至11点设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).

(1)求此次拦查中醉酒驾车的人数;
(2)从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,再从抽取的8人中任取3人,求3人中含有醉酒驾车人数X的分布列和数学期望.
【答案】(1)15人;(2)渐近线.
【解析】试题分析:(1)由频率分布直方图得小长方形面积等于对应频率,再根据频数等于总数乘以频率得结果(2)先按分层抽样得含有醉酒驾车者人数,再确定随机变量,利用组合数逐个求对应概率,列表可得分布列,最后根据数学期望公式求期望
试题解析:(1)由已知得,(0.003 2+0.004 3+0.005 0)×20=0.25,0.25×60=15,所以此次拦查中醉酒驾车的人数为15人.
(2)易知利用分层抽样抽取8人中含有醉酒驾车者为2人,所以X的所有可能取值为0,1,2.
P(X=0)=![]() =
=![]() ,P(X=1)=
,P(X=1)=![]() =
=![]() ,
,
P(X=2)=![]() =
=![]() ,
,
X的分布列为
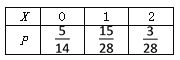
E(X)=0×![]() +1×
+1×![]() +2×
+2×![]() =
=![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cos2B+cosB=1-cosAcosC.
(1)求证:a,b,c成等比数列;
(2)若b=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中:
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量![]() ,则对于空间的任意一个向量
,则对于空间的任意一个向量![]() ,总存在实数x,y,z,使得
,总存在实数x,y,z,使得![]() 。
。
正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切圆M于A,B两点。
(1)若Q(1,0),求切线QA,QB的方程;
(2)求四边形QAMB面积的最小值;
(3)若|AB|=![]() ,求直线MQ的方程。
,求直线MQ的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a为实数).
(a为实数).
(1) 若函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求实数a的值;
平行,求实数a的值;
(2) 若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3) 若函数![]() 在区间
在区间![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年一交警统计了某段路过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:
车速 |
|
|
|
|
|
事故次数 |
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(参考数据:![]() )
)
[参考公式: ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
先由命题解![]() 得
得![]() ;命题
;命题![]() 得
得![]() ,
,
(1)当![]() ,得命题
,得命题![]() ,再由
,再由![]() 为真,得
为真,得![]() 真且
真且![]() 真,即可求解
真,即可求解![]() 的取值范围.
的取值范围.
(2)由![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的充分必要条件,根据则
的充分必要条件,根据则![]()
![]() ,即可求解实数
,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
命题![]() :由题得
:由题得![]() ,又
,又![]() ,解得
,解得![]() ;
;
命题![]() :
: ![]() ,解得
,解得![]() .
.
(1)若![]() ,命题
,命题![]() 为真时,
为真时, ![]() ,
,
当![]() 为真,则
为真,则![]() 真且
真且![]() 真,
真,
∴![]() 解得
解得![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的充分必要条件,
的充分必要条件,
设![]() ,
, ![]() ,则
,则![]()
![]() ;
;
∴![]() ∴实数
∴实数![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线顶点在原点,焦点在![]() 轴上,又知此抛物线上一点
轴上,又知此抛物线上一点![]() 到焦点的距离为6.
到焦点的距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 中点横坐标为2,求
中点横坐标为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com