
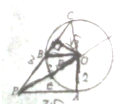
 如图,已知⊙O的半径为2,PA是⊙O的切线,A为切点,且PA=2
如图,已知⊙O的半径为2,PA是⊙O的切线,A为切点,且PA=2| 2 |
| 3 |
科目:高中数学 来源: 题型:
|
| A、3n2+3n |
| B、3×2n+2+9 |
| C、3n+2+6 |
| D、9×2n+1-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、从匀速快递的产品生产流水线上,质检员每15分钟从中抽取一样产品进行某项指标检测,这样的抽样是系统抽样 |
| B、对分类变量X与Y的随机变量K2的观测值k来说,k越大,“X与Y有关系”的把握程度越大 |
| C、两个随机变量相关越强,则相关系数的绝对值越接近于0 |
| D、在回归直线方程y=0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、ln2 | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
cos
| ||
sin
|
| α |
| 2 |
| 1-cos2α |
| 2sinα |
| π |
| 4 |
| 6 |
| 5 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com