
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位在2019年重阳节组织50名退休职工(男、女各25名)旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表:
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
(1)据此资料分析,是否有![]() 的把握认为选择哪个景点与性别有关?
的把握认为选择哪个景点与性别有关?
(2)按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附: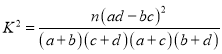 ,
,![]() .
.
P( | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 上一点
上一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() ,
, ![]() 的面积为
的面积为![]() ,直线
,直线![]() 过
过![]() 上的点
上的点![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 为
为![]() 的短轴端点,直线
的短轴端点,直线![]() 过点
过点![]() 交
交![]() 于
于![]() ,证明:四边形
,证明:四边形![]() 的两条对角线的交点在定直线上.
的两条对角线的交点在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,海岸公路MN的北方有一个小岛A(大小忽略不计)盛产海产品,在公路MN的B处有一个海产品集散中心,点C在B的正西方向10![]() 处,
处,![]() ,
,![]() ,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/
,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/![]() 、200元/
、200元/![]() .
.
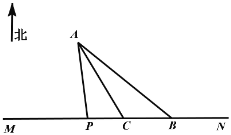
(1)求方案①的运输费用;
(2)请确定P点的位置,使得按方案②运送时运输费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)在(﹣∞,0]上单调递增,且f(﹣1)=﹣1.若f(x﹣1)+1≥0,则x的取值范围是_____;设函数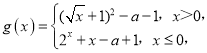 若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
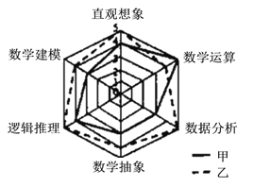
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com