
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的 500 名志愿者中随机抽取 100 名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是[20,25),[25,30),[30,35),[35,40),[40,45].
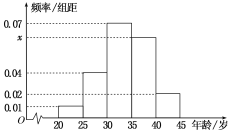
(1)求图中x的值并根据频率分布直方图估计这 500 名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 20 名参加中心广场的宣传活动,再从这 20 名中采用简单随机抽样方法选取 3 名志愿者担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 X,求 X 的分布列及均值.
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向
向
圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.
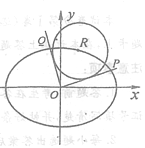
(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
(3)试问![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图所示的率分布直方图,
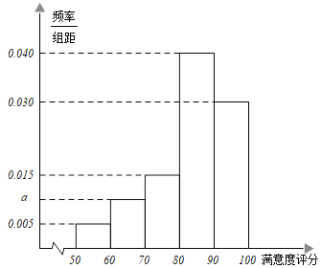
(1)求频率分布直方图中![]() 的值
的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为![]() .
.
(1)从袋中随机抽取两个球,求取出的球的编号之和为偶数的概率;
(2)先从袋中随机取一个球,该球的编号为![]() ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从
大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从![]() 届的毕业生中,抽取了本科和研究生毕业生各
届的毕业生中,抽取了本科和研究生毕业生各![]() 名,得到下表中的数据.
名,得到下表中的数据.
就业专业 毕业学历 | 就业为所学专业 | 就业非所学专业 |
本科 |
|
|
研究生 |
|
|
(1)根据表中的数据,能否在犯错概率不超过![]() 的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
(2)为了进一步分析和了解本科毕业生就业的问题,按分层抽样的原则从本科毕业生中抽取一个容量为![]() 的样本,要从
的样本,要从![]() 人中任取
人中任取![]() 人参加座谈,求被选取的
人参加座谈,求被选取的![]() 人中至少有
人中至少有![]() 人就业非毕业所学专业的概率.
人就业非毕业所学专业的概率.
附: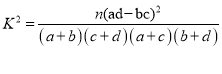 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 的单调递减区间;
的单调递减区间;
②当![]() 时,直线y=k与y=f (x)的图象有两个不同交点;
时,直线y=k与y=f (x)的图象有两个不同交点;
③函数y=f(x)的图象与![]() 的图象没有公共点;
的图象没有公共点;
④当![]() 时,函数
时,函数![]() 的最小值为2.
的最小值为2.
其中正确结论的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贵阳河滨公园是市民休闲游玩的重要场所,某校社团针对“公园环境评价”随机对![]() 位市民进行问卷调查打分(满分100分)得茎叶图如下:
位市民进行问卷调查打分(满分100分)得茎叶图如下:

(1)写出女性打分的中位数和众数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民中随机请
分)的市民中随机请![]() 人进一步提建议,求这
人进一步提建议,求这![]() 人都是男性市民的概率.
人都是男性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 为真,
为真,![]() 为假,
为假,![]() 为真
为真
(2)“![]() ”是“曲线
”是“曲线![]() 表示椭圆”的充要条件
表示椭圆”的充要条件
(3)命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
(4)如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
则正确命题有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com