
思路解析:双曲线上一点与焦点的连线问题,常考虑焦半径比较简单.
(1)解法一:∵BF=![]() =3
=3![]() ,|AF|=
,|AF|=![]() ,又∵A(x1,y1)在双曲线上,∴x12=
,又∵A(x1,y1)在双曲线上,∴x12=![]() .∴|AF|2=x12+(y1-5)2=
.∴|AF|2=x12+(y1-5)2=![]() +(y1-5)2=
+(y1-5)2=![]() (5y1-12)2,由A、B、C在双曲线的同一支上,即上半支上.∴y1≥2
(5y1-12)2,由A、B、C在双曲线的同一支上,即上半支上.∴y1≥2![]() ,5y1-12>0.∴AF=
,5y1-12>0.∴AF=![]() (5y1-12).同理可求得CF=
(5y1-12).同理可求得CF=![]() (5y2-12),由于AF+CF=2BF,∴
(5y2-12),由于AF+CF=2BF,∴![]() (5y1-12)+
(5y1-12)+![]() (5y2-12)=6
(5y2-12)=6![]() .∴y1+y2=12.
.∴y1+y2=12.
解法二:∵双曲线的实半轴长为a=2![]() ,虚半轴b=
,虚半轴b=![]() ,半焦距c=5,与焦点F(0,5)对应的准线方程为y=
,半焦距c=5,与焦点F(0,5)对应的准线方程为y=![]() .由双曲线第二定义知,
.由双曲线第二定义知,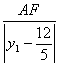 =
=![]() ,
,
∵y1≥2![]() ,∴y1-
,∴y1-![]() >0.∴|AF|=
>0.∴|AF|=![]() (y1-
(y1-![]() ).
).
同理CF=![]() ·(y1-
·(y1-![]() ),|BF|=
),|BF|=![]() (6-
(6-![]() )=3
)=3![]() .
.
∵|AF|+|CF|=2|BF|,∴y1+y2=12.
解法三:双曲线的离心率e=![]() =
=![]() ,|AF|=|ey1-a|=ey1-a,|CF|=|ey2-a|=ey2-a,|BF|=
,|AF|=|ey1-a|=ey1-a,|CF|=|ey2-a|=ey2-a,|BF|=![]() ×6-2
×6-2![]() =3
=3![]() ,又∵|AF|+|CF|=2|BF|=6
,又∵|AF|+|CF|=2|BF|=6![]() ,
,
∴e(y1+y2)-2a=6![]() .∴y1+y2=12.
.∴y1+y2=12.
(2)证明:线段AC中点M(![]() ,6),kAC=
,6),kAC=![]() ,∴线段AC的垂直平分线方程为y-6=
,∴线段AC的垂直平分线方程为y-6=![]() (x-
(x-![]() )=
)=![]() x-
x-![]() . ①
. ①
∵![]() -
-![]() =1,
=1,![]() -
-![]() =1,两式相减,得x12-x22=
=1,两式相减,得x12-x22=![]() (y12-y22),
(y12-y22),
又∵y1+y2=12,∴x12-x22=13(y1-y2).代入①,
得y-6=![]() x+
x+![]() .
.
∴y-![]() =
=![]() x.∴恒过点(0,
x.∴恒过点(0,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
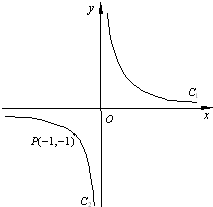 设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.
设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com