Question

19．设a∈R，函数f（x）=x|x-a|+2x．
（1）若a=3，求函数f（x）在区间[0，4]上的最大值；
（2）若存在a∈（2，4]，使得关于x的方程f（x）=t•f（a）有三个不相等的实数解，求实数t的取值范围．

Answer 1

分析 （1）求出f（x）的分段函数式，运用二次函数的性质，可得单调区间，求得最大值；
（2）将x分区间进行讨论，去绝对值写出解析式，求出单调区间，将a分区间讨论，求出单调区间解出即可．

解答 解：（1）当a=3，x∈[0，4]时，f（x）=x|x-3|+2x=$\left\{\begin{array}{l}{{x}^{2}-x，3≤x≤4}\\{5x-{x}^{2}，0≤x＜3}\end{array}\right.$，
可知函数f（x）在区间[0，$\frac{5}{2}$]递增，在（$\frac{5}{2}$，3]上是减函数，在[3，4]递增，
则f（$\frac{5}{2}$）=$\frac{25}{4}$，f（4）=12，
所以f（x）在区间[0，4]上的最大值为f（4）=12．
（2）f（x）=$\left\{\begin{array}{l}{{x}^{2}+（2-a）x，x≥a}\\{-{x}^{2}+（2+a）x，x＜a}\end{array}\right.$，
①当x≥a时，因为a＞2，所以$\frac{a-2}{2}$＜a．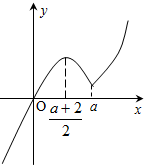
所以f（x）在[a，+∞）上单调递增．
②当x＜a时，因为a＞2，所以$\frac{a+2}{2}$＜a．
所以f（x）在（-∞，$\frac{a+2}{2}$）上单调递增，在[$\frac{a+2}{2}$，a]上单调递减．
当2＜a≤4时，知f（x）在（-∞，$\frac{a+2}{2}$]和[a，+∞）上分别是增函数，
在[$\frac{a+2}{2}$，a]上是减函数，
当且仅当2a＜t•f（a）＜$\frac{（a+2）^{2}}{4}$时，
方程f（x）=t•f（a）有三个不相等的实数解．
即1＜t＜$\frac{（a+2）^{2}}{8a}$=$\frac{1}{8}$（a+$\frac{4}{a}$+4）．
令g（a）=a+$\frac{4}{a}$，g（a）在a∈（2，4]时是增函数，
故g（a）_max=5．
∴实数t的取值范围是（1，$\frac{9}{8}$）．

点评 本题考查了函数的最值，函数单调性的证明，渗透了分类讨论思想，综合性较强，是较难的一道题．