
分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形求出p即可.
解答 解:抛物线的焦点坐标为($\frac{p}{2}$,0),准线方程为:x=-$\frac{p}{2}$,
准线方程与双曲线y2-x2=1联立可得:y2-(-$\frac{p}{2}$)2=1,
解得y=±$\sqrt{1+\frac{{p}^{2}}{4}}$,
因为△ABF为等边三角形,所以$\sqrt{{y}^{2}+{p}^{2}}$=2|y|,即p2=3y2,
即p2=3(1+$\frac{{p}^{2}}{4}$),解得p=$2\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题

| A. | ①⑤⑥,②③④ | B. | ①③⑤,②④⑥ | C. | ①②③,④⑤⑥ | D. | ①②⑥,③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M1=M2=M3=M4 | B. | M1?M2?M3?M4 | C. | M1⊆M2⊆M3⊆M4 | D. | M2⊆M3且M2⊆M4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
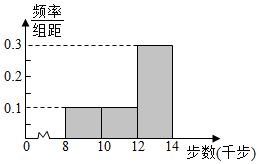 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
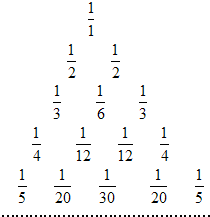 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com