
【题目】已知函数![]() 和
和![]() 同时满足以下两个条件:
同时满足以下两个条件:
(1)对于任意实数![]() ,都有
,都有![]() 或
或![]() ;
;
(2)总存在![]() ,使
,使![]() 成立.
成立.
则实数![]() 的取值范围是 __________.
的取值范围是 __________.
【答案】![]()
【解析】
由于g(x)=![]() ≥0时,x≥3,根据题意有f(x)=m(x﹣m)(x+2m+3)<0在x≥3时成立;由于x∈(﹣∞,﹣1),f(x)g(x)<0,而g(x)=3x﹣3<0,则f(x)=m(x﹣m)(x+2m+3)>0在x∈(﹣∞,﹣1)时成立.由此结合二次函数的性质可求出结果.
≥0时,x≥3,根据题意有f(x)=m(x﹣m)(x+2m+3)<0在x≥3时成立;由于x∈(﹣∞,﹣1),f(x)g(x)<0,而g(x)=3x﹣3<0,则f(x)=m(x﹣m)(x+2m+3)>0在x∈(﹣∞,﹣1)时成立.由此结合二次函数的性质可求出结果.
对于①∵g(x)=![]() ,当x<3时,g(x)<0,
,当x<3时,g(x)<0,
又∵①x∈R,f(x)<0或g(x)<0
∴f(x)=m(x﹣m)(x+2m+3)<0在x≥3时恒成立
则由二次函数的性质可知开口只能向下,且二次函数与x轴交点都在(3,0)的左面,
即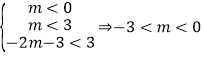 可得﹣3<m<0
可得﹣3<m<0
又∵②x∈(﹣∞,﹣1),f(x)g(x)<0
∴此时g(x)=![]() <0恒成立
<0恒成立
∴f(x)=m(x﹣m)(x+m+2)>0在x∈(﹣∞,﹣1)有成立的可能,
则只要﹣1比x1,x2中的较小的根大即可,
(i)当﹣1<m<0时,较小的根为﹣2m﹣3,f(x)=m(x﹣m)(x+m+2)>0在x∈(﹣∞,﹣1)有成立的可能,
(ii)当m=﹣1时,两个根同为﹣1,f(x)<0在区间![]() 内恒成立,故不满足题意。
内恒成立,故不满足题意。
(iii)当﹣3<m<﹣1时,较小的根为m,f(x)=m(x﹣m)(x+m+2)>0在x∈(﹣∞,﹣1)有成立的可能,
综上可得①②成立时﹣3<m<﹣1或-1<m<0.
故答案为:![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足
是单调函数。如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 为全集).
为全集).
查看答案和解析>>
科目:高中数学 来源: 题型:
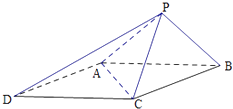
【题目】如图,已知四棱锥P﹣ABCD的底面ABCD为菱形,且∠ABC=60°,
AB=PC=2,PA=PB= ![]() .
.
(1)求证:平面PAB⊥平面ABCD;
(2)设H是PB上的动点,求CH与平面PAB所成最大角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要制作一个容积为8m3 , 高为2m的无盖长方体容器,若容器的底面造价是每平方米200元,侧面造型是每平方米100元,则该容器的最低总造价为( )
A.1200元
B.2400元
C.3600元
D.3800元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t![]() 1,不等式f(
1,不等式f(![]() )+f(
)+f(![]() )<0恒成立,求k的取值范围.
)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中与f(x)=x是同一函数的有( )
①y=![]() ②y=
②y=![]() ③y=
③y=![]() ④y=
④y=![]() ⑤f(t)=t⑥g(x)=x
⑤f(t)=t⑥g(x)=x
A. 1 个 B. 2 个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“招手即停”公共汽车的票价按下列规则制定:
5公里以内(含5公里),票价2元;
5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,请根据题意.
(1)写出票价与里程之间的函数解析式;
(2)根据(1)写出的函数解析式试画出该函数的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com