
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a(a∈R)在其定义域内有两个不同的极值点.
x2﹣x+a(a∈R)在其定义域内有两个不同的极值点.
(Ⅰ)求a的取值范围;
(Ⅱ)设两个极值点分别为x1 , x2 , 证明:x1x2>e2 .
【答案】解:(Ⅰ)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根;
即方程lnx﹣ax=0在(0,+∞)有两个不同根;
(解法一)转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如右图.
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0= ![]() ,又k=
,又k= ![]() ,
,
故 ![]() =
= ![]() ,
,
解得,x0=e,
故k= ![]() ,
,
故0<a< ![]() .
.
(解法二)转化为函数g(x)= ![]() 与函数y=a的图象在(0,+∞)上有两个不同交点.
与函数y=a的图象在(0,+∞)上有两个不同交点.
又g′(x)= ![]() ,
,
即0<x<e时,g′(x)>0,x>e时,g′(x)<0,
故g(x)在(0,e)上单调增,在(e,+∞)上单调减.
故g(x)极大=g(e)= ![]() ;
;
又g(x)有且只有一个零点是1,且在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→0,
故g(x)的草图如右图,
可见,要想函数g(x)= ![]() 与函数y=a的图象在(0,+∞)上有两个不同交点,
与函数y=a的图象在(0,+∞)上有两个不同交点,
只须0<a< ![]() .
.
(解法三)令g(x)=lnx﹣ax,从而转化为函数g(x)有两个不同零点,
而g′(x)= ![]() ﹣ax=
﹣ax= ![]() (x>0),
(x>0),
若a≤0,可见g′(x)>0在(0,+∞)上恒成立,所以g(x)在(0,+∞)单调增,
此时g(x)不可能有两个不同零点.
若a>0,在0<x< ![]() 时,g′(x)>0,在x>
时,g′(x)>0,在x> ![]() 时,g′(x)<0,
时,g′(x)<0,
所以g(x)在(0, ![]() )上单调增,在(
)上单调增,在( ![]() ,+∞)上单调减,从而g(x)极大=g(
,+∞)上单调减,从而g(x)极大=g( ![]() )=ln
)=ln ![]() ﹣1,
﹣1,
又因为在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→﹣∞,
于是只须:g(x)极大>0,即ln ![]() ﹣1>0,所以0<a<
﹣1>0,所以0<a< ![]() .
.
综上所述,0<a< ![]() .
.
(Ⅱ)由(Ⅰ)可知x1,x2分别是方程lnx﹣ax=0的两个根,
即lnx1=ax1,lnx2=ax2,
设x1>x2,作差得ln ![]() =a(x1﹣x2),即a=
=a(x1﹣x2),即a= ![]()
原不等式 ![]() 等价于ln
等价于ln ![]() >
> ![]() ,
,
令 ![]() ,则t>1,
,则t>1, ![]() ,
,
设 ![]() ,
, ![]() ,
,
∴函数g(t)在(1,+∞)上单调递增,
∴g(t)>g(1)=0,
即不等式 ![]() 成立,
成立,
故所证不等式 ![]() 成立.
成立.


【解析】(Ⅰ)将函数f(x)在其定义域内有两个不同的极值点转化为其导函数在(0,+∞)有两个不同根进行解题;(Ⅱ)将问题变为对函数增减性的证明,可以先从所要证的结论出发进行分析,进而证明.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() :
: ![]() .
.
(1)设点![]() 是直线
是直线![]() 上的一动点,过
上的一动点,过![]() 点作圆
点作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 的面积的最小值;
的面积的最小值;
(2)过![]() 作直线
作直线![]() 的垂线交圆
的垂线交圆![]() 于
于![]() 点,
点, ![]() 为
为![]() 关于
关于![]() 轴的对称点,若
轴的对称点,若![]() 是圆
是圆![]() 上异于
上异于![]() 的两个不同点,且满足:
的两个不同点,且满足: ![]() ,试证明直线
,试证明直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2﹣f(﹣x),当x∈(﹣∞,0)时,f′(x)+ ![]() <4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
<4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
A.[﹣ ![]() ,+∞)
,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Ω={(x,y)|0≤x≤1,0≤y≤1},A是由直线y=0,x=a(0<a≤1)和曲线y=x3围成的曲边三角形的平面区域,若向区域Ω上随机投一点P,点P落在区域A内的概率是 ![]() ,则a的值为( )
,则a的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A.回归直线一定过样本中心( ![]() )
)
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.两个模型中残差平方和越小的模型拟合的效果越好
D.甲、乙两个模型的R2分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 ![]() ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.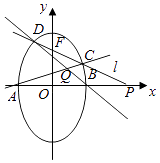
(Ⅰ)当 ![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com