
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意的![]() 和
和![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了![]() 人,患有呼吸系统疾病的
人,患有呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.没有患呼吸系统疾病的
人在室内工作.没有患呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.
人在室内工作.
(1)现采用分层抽样从室内工作的居民中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
(2)你能否在犯错误率不超过![]() 的前提下认为感染呼吸系统疾病与工作场所有关;
的前提下认为感染呼吸系统疾病与工作场所有关;
附表:
|
|
|
|
|
|
|
|
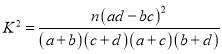
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排6名同学前往4所学校进行演讲,要求甲、乙两同学不能前往同一个学校,每个学校都有人前往,每人只前往一个学校,则满足上述要求的不同安排方案数为________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
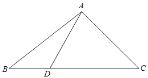
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() .过
.过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() (不与点
(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com