�٢�
�������ٽ�����B���оٷ���ʾ�����ý����Ķ����â���ȷ������ֱ�ߴ�ֱ�ij�Ҫ����Ϊa+3b=0���ʿ��þٷ������ų��ڣ���ֻ�����������С��A�ķ�Χ�������ж�����ֵһ�������㣬�ų��ۣ��ܽ����Ƿ��̼��ɵ�����㣻�����û�����ʽ�������ΰ뾶���������������ʽ����������������
��𣺢١�A=[0��1]��B={1��2��3��4��5��6��7��8��9}����A��B={1}������ȷ��
�ڵ�a=0��b=0ʱ����ֱ�ߴ�ֱ����

�����壬�ڴ���
�ۡ�A�ʣ�0���У�����sinA��0���֡�
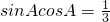
��0����cosA��0����A�ʣ�0��

������sinA+cosA��0�������ܵ���
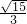
���۴���
�ܡ�f��x��=|sinx|=0?sinx=0?x=k�У���k��Z�����ຯ��f��x��=|sinx|�����Ϊk�У�k��Z��������ȷ��
�ݡ���l=|��|��r����4=2��r�����Բ�뾶r=2�������ε����s=

lr�������Բ�Ľ��������ε����Ϊ

��4��2=4cm
2���ݴ���
�ʴ�Ϊ �٢�
�����������ۺϿ����˼��ϵı�ʾ�����������㣬��ֱ�ߵ�λ�ù�ϵ��ֱ�߷��̣��������е����Ǻ���ֵ�ļ��㣬���Һ�������㼰�������µĻ�������������ļ��㹫ʽ�Ȼ���֪ʶ

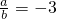 ��
��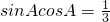 ����
����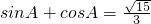 ��
�� �����壬�ڴ���
�����壬�ڴ���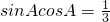 ��0����cosA��0����A�ʣ�0��
��0����cosA��0����A�ʣ�0�� ������sinA+cosA��0�������ܵ���
������sinA+cosA��0�������ܵ���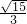 ���۴���
���۴��� lr�������Բ�Ľ��������ε����Ϊ
lr�������Բ�Ľ��������ε����Ϊ ��4��2=4cm2���ݴ���
��4��2=4cm2���ݴ���

 ��У����ϵ�д�
��У����ϵ�д�